题目内容
已知AB是⊙O的直径，点C在⊙O上，连接AC，BC，若∠A=30°，则∠B为
- A.30°
- B.45°
- C.60°
- D.90°
C
分析：根据直径所对圆周角等于90°，以及两角互余求出∠B即可．
解答：
解：∵AB是⊙O的直径，点C在⊙O上，∠A=30°，
∴∠ACB=90°，
∴∠B=90°-30°=60°，
故选：C．
点评：此题主要考查了圆周角定理，根据已知画出图形进而得出∠ACB=90°是解题关键．
分析：根据直径所对圆周角等于90°，以及两角互余求出∠B即可．
解答：
解：∵AB是⊙O的直径，点C在⊙O上，∠A=30°，∴∠ACB=90°，
∴∠B=90°-30°=60°，
故选：C．
点评：此题主要考查了圆周角定理，根据已知画出图形进而得出∠ACB=90°是解题关键．
练习册系列答案
天天向上一本好卷系列答案
相关题目
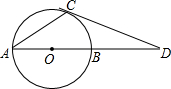如图，已知AB是⊙O的直径，∠CAB=30°，过点C的⊙O的切线交AB延长线于D，若OD=
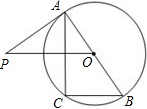如图，已知AB是⊙O的直径，过点O作弦BC的平行线，交过点A的切线AP于点P，连接AC．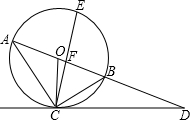
如图，已知AB是⊙O的直径，AD切⊙O于点A，