题目内容
解方程:
解:设 ,则原方程为y+
,则原方程为y+ =3,
=3,
去分母得y2-3y+2=0,
解得y1=1,y2=2.
由 得x2-x+1=0,
得x2-x+1=0,
∵△=(-1)2-4×1×1<0,∴这个方程无实数根.
由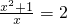 得x2-2x+1=0解得x1=x2=1
得x2-2x+1=0解得x1=x2=1
经检验,x1=x2=1是原方程的根.
∴原方程的根是x1=x2=1.
分析:方程的两个部分具备倒数关系,设 ,则原方程另一个分式为
,则原方程另一个分式为 .可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
.可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
点评:换元法解分式方程时常用方法之一,它能够把一些分式方程化繁为简,化难为易,对此应注意总结能用换元法解的分式方程的特点,寻找解题技巧.
 ,则原方程为y+
,则原方程为y+ =3,
=3,去分母得y2-3y+2=0,
解得y1=1,y2=2.
由
 得x2-x+1=0,
得x2-x+1=0,∵△=(-1)2-4×1×1<0,∴这个方程无实数根.
由
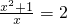 得x2-2x+1=0解得x1=x2=1
得x2-2x+1=0解得x1=x2=1经检验,x1=x2=1是原方程的根.
∴原方程的根是x1=x2=1.
分析:方程的两个部分具备倒数关系,设
 ,则原方程另一个分式为
,则原方程另一个分式为 .可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
.可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.点评:换元法解分式方程时常用方法之一,它能够把一些分式方程化繁为简,化难为易,对此应注意总结能用换元法解的分式方程的特点,寻找解题技巧.

练习册系列答案
相关题目