题目内容
【题目】如图,已知抛物线![]() 与y轴交于点
与y轴交于点![]() ,与x轴交于点
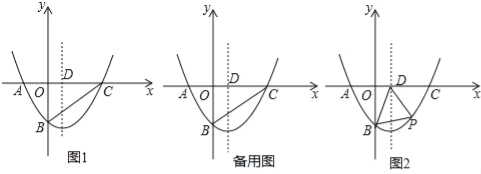
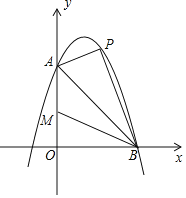
,与x轴交于点![]() ,点P是线段AB上方抛物线上的一个动点.
,点P是线段AB上方抛物线上的一个动点.
![]() 求这条抛物线的表达式及其顶点坐标;
求这条抛物线的表达式及其顶点坐标;
![]() 当点P移动到抛物线的什么位置时,使得
当点P移动到抛物线的什么位置时,使得![]() ,求出此时点P的坐标;
,求出此时点P的坐标;
![]() 当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动;与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止
当点P从A点出发沿线段AB上方的抛物线向终点B移动,在移动中,点P的横坐标以每秒1个单位长度的速度变动;与此同时点M以每秒1个单位长度的速度沿AO向终点O移动,点P,M移动到各自终点时停止![]() 当两个动点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少?
当两个动点移动t秒时,求四边形PAMB的面积S关于t的函数表达式,并求t为何值时,S有最大值,最大值是多少?
【答案】(1)抛物线的表达式为![]() ,抛物线的顶点坐标为
,抛物线的顶点坐标为![]() ;(2)P点坐标为
;(2)P点坐标为![]() ;(3)当
;(3)当![]() 时,S有最大值,最大值为24.
时,S有最大值,最大值为24.
【解析】分析:(1)由A、B坐标,利用待定系数法可求得抛物线的表达式,化为顶点式可求得顶点坐标;
(2)过P作PC⊥y轴于点C,由条件可求得∠PAC=60°,可设AC=m,在Rt△PAC中,可表示出PC的长,从而可用m表示出P点坐标,代入抛物线解析式可求得m的值,即可求得P点坐标;
(3)用t可表示出P、M的坐标,过P作PE⊥x轴于点E,交AB于点F,则可表示出F的坐标,从而可用t表示出PF的长,从而可表示出△PAB的面积,利用S四边形PAMB=S△PAB+S△AMB,可得到S关于t的二次函数,利用二次函数的性质可求得其最大值.
详解:![]() 根据题意,把
根据题意,把![]() ,
,![]() 代入抛物线解析式可得
代入抛物线解析式可得![]() ,解得
,解得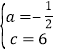 ,
,
![]() 抛物线的表达式为
抛物线的表达式为![]() ,
,
![]() ,
,
![]() 抛物线的顶点坐标为
抛物线的顶点坐标为![]() ;
;
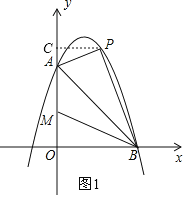
![]() 如图1,过P作
如图1,过P作![]() 轴于点C,
轴于点C,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
把P点坐标代入抛物线表达式可得![]() ,解得
,解得![]() 或
或![]() ,
,
经检验,![]() 与点A重合,不合题意,舍去,
与点A重合,不合题意,舍去,
![]() 所求的P点坐标为
所求的P点坐标为![]() ;
;
![]() 当两个动点移动t秒时,则
当两个动点移动t秒时,则![]() ,
,![]() ,
,
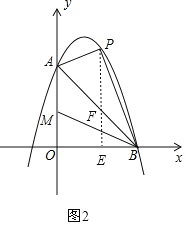
如图2,作![]() 轴于点E,交AB于点F,则
轴于点E,交AB于点F,则![]() ,
,
![]() ,
,
![]() ,
,
![]() 点A到PE的距离竽OE,点B到PE的距离等于BE,
点A到PE的距离竽OE,点B到PE的距离等于BE,
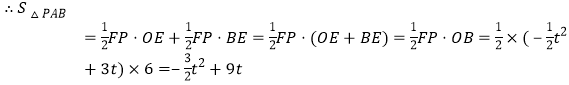 ,且
,且![]() ,
,
![]() ,
,
![]() 当
当![]() 时,S有最大值,最大值为24.
时,S有最大值,最大值为24.

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.