题目内容
已知:如图,Rt△ABC,∠ACB=90°,点E是边BC上一点,过点E作FE⊥BC(![]() 垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E交BC于点D
垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E交BC于点D
(1)求证:直线AB是⊙E的切线;
(2)设直线AB和⊙E的公共点为G, AC=8,EF=5,连DG,求⊙E的半径r.
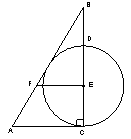
(1)证明:连接AE,过E作EG⊥AB于G,
∵FE⊥BC ∴∠BEF=90°
又∠ACB=90°
∴EF∥AC ∴∠AEF=∠EAC
∵EF=AF ∴∠AEF=∠EAF
∴∠EAC![]() =∠EAF
=∠EAF
∵∠ACB=90 ∴EC⊥AC
又EG⊥AB
∴EG =![]() EC
EC
∴直线AB是⊙E的切线.
(2)解:∵EC⊥AC,
∴直线AC是⊙E的切线
又直线AB是⊙E的切线(已证),切点为G,
∴AG=AC=8
又AE=EF=5
∴FG=AG—AF = 3
在Rt△EFG中,
![]()
∴⊙E的半径r的长为4.

练习册系列答案
相关题目


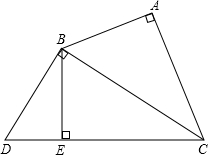 已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.
已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4. 22、已知:如图Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.
22、已知:如图Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.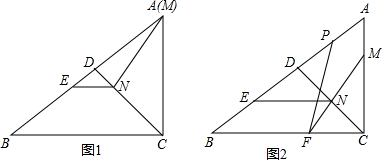
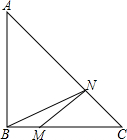 已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为
已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为