题目内容
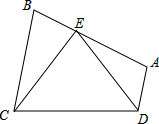 如图,四边形ABCD中,BC∥AD,E为AB上一点,且EC=ED,∠CED=∠B
如图,四边形ABCD中,BC∥AD,E为AB上一点,且EC=ED,∠CED=∠B(1)猜想BE与AD的数量关系,并说明理由;
(2)如果将“BC∥AD”改为“∠CED=∠B=2∠A=2a”,其它条件不变,上述结论还成立吗?画出图形,进行探究.
考点:全等三角形的判定与性质
专题:
分析:(1)延长EA到F,使EF=BC,易证∠BCE=∠AED,可以证明△CBE≌△FED,可得∠B=∠F,BE=DF,即可求得DA=DF=BE;
(2)在EA上截取EF=BC,易证∠BCE=∠AED,可以证明△CBE≌△FED,可得BE=DF,即可证明∠ADF=∠A=α,AF=DF,再分类讨论:①若∠A=60°,②若∠A<60°,③若∠A>60°,即可解题.
(2)在EA上截取EF=BC,易证∠BCE=∠AED,可以证明△CBE≌△FED,可得BE=DF,即可证明∠ADF=∠A=α,AF=DF,再分类讨论:①若∠A=60°,②若∠A<60°,③若∠A>60°,即可解题.
解答:证明:(1)延长EA到F,使EF=BC,
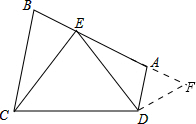
∵∠B∠CED,∠B+∠BCE=∠CED+∠AED,
∴∠BCE=∠AED,
∵在△CBE和△FED中,
,
∴△CBE≌△FED,(SAS)
∴∠B=∠F,BE=DF,
∵BC∥AD,
∴∠B+∠A=180°,
∵∠FAD+∠A=180°,
∴∠FAD=∠B=∠F,
∴DA=DF=BE;
(2)在EA上截取EF=BC,
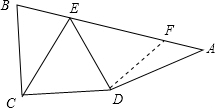
∵∠B=∠CED,∠B+∠BCE=∠CED+∠AED,
∴∠BCE=∠AED,
∵在△CBE和△FED中,
,
∴△CBE≌△FED,(SAS)
∴BE=DF,
∵∠B=∠EFD=2α,∠A=α,
∴∠ADF=∠A=α,AF=DF,
讨论:①若∠A=60°,则EF=AD=BE,
②若∠A<60°,则AD<EF=BE,
③若∠A>60°,则AD>EF=BE.

∵∠B∠CED,∠B+∠BCE=∠CED+∠AED,
∴∠BCE=∠AED,
∵在△CBE和△FED中,
|
∴△CBE≌△FED,(SAS)
∴∠B=∠F,BE=DF,
∵BC∥AD,
∴∠B+∠A=180°,
∵∠FAD+∠A=180°,
∴∠FAD=∠B=∠F,
∴DA=DF=BE;
(2)在EA上截取EF=BC,

∵∠B=∠CED,∠B+∠BCE=∠CED+∠AED,
∴∠BCE=∠AED,
∵在△CBE和△FED中,
|
∴△CBE≌△FED,(SAS)
∴BE=DF,
∵∠B=∠EFD=2α,∠A=α,
∴∠ADF=∠A=α,AF=DF,
讨论:①若∠A=60°,则EF=AD=BE,
②若∠A<60°,则AD<EF=BE,
③若∠A>60°,则AD>EF=BE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△CBE≌△FED是解题的关键.

练习册系列答案
相关题目
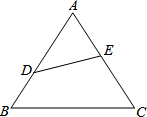 如图,等边△ABC的边长为1,D、E两点分别在边AB、AC上,CE=DE,则线段CE的最小值为( )
如图,等边△ABC的边长为1,D、E两点分别在边AB、AC上,CE=DE,则线段CE的最小值为( )A、2-
| ||||
B、2
| ||||
C、
| ||||
D、
|
下列式子是分式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若把分式
的x、y同时扩大10倍,则分式的值( )
| x+3y |
| 2x |
| A、扩大10倍 | B、缩小10倍 |
| C、不变 | D、缩小5倍 |
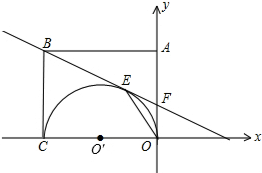 如图,矩形OABC的两边OC、OA分别是x轴和y轴上,过点B的直线切以OC为直径的半圆O′于点E,交y轴于点F,连接OE,且已知C(-6,0),F(0,2).试求点B的坐标.
如图,矩形OABC的两边OC、OA分别是x轴和y轴上,过点B的直线切以OC为直径的半圆O′于点E,交y轴于点F,连接OE,且已知C(-6,0),F(0,2).试求点B的坐标.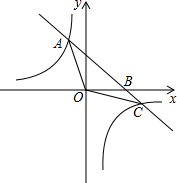 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y=