题目内容
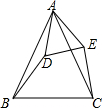 如图:△ABC、△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?
如图:△ABC、△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?
分析:由图可知,△ABD≌△ACE,所以两个三角形可以通过旋转相互得到.
解答:解:∵△ABC、△ADE均是顶角为42°的等腰三角形,
∴∠BAC=∠DAE=42°,
∴∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∴△ABD≌△ACE,
∴△ABD与△ACE可通过旋转相互得到,
△ABD可以点A为旋转中心,逆时针旋转42°,使△ABD与△ACE重合.
∴∠BAC=∠DAE=42°,
∴∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE,
∴△ABD与△ACE可通过旋转相互得到,
△ABD可以点A为旋转中心,逆时针旋转42°,使△ABD与△ACE重合.
点评:熟练掌握等腰三角形及等边三角形的性质,能够熟练解决一些简单的旋转,翻折问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
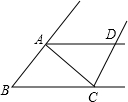 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
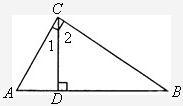
 ,且CB=CE.
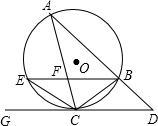
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.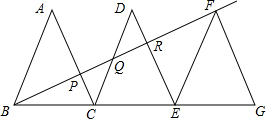 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且