Question

【题目】在中，，射线，点在射线上（不与点重合），连接，过点作的垂线交的延长线于点．

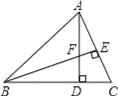
（1）如图①，若，且，求的度数；

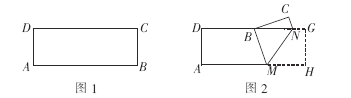
（2）如图②，若，当点在射线上运动时，与之间有怎样的数量关系？请写出你的结论，并加以证明．

（3） 如图③，在（2）的条件下，连接，设与射线的交点为，，，当点在射线上运动时，与之间有怎样的数量关系？请写出你的结论，并加以证明．

Answer 1

【答案】（1）；（2），见解析；（3），见解析

【解析】

（1）如图①中，首先证明△ABD是等边三角形，推出∠ABD=60°，由∠PDB+∠PAB=180°，推出∠APD+∠ABD=180°，由此即可解决问题．

（2）如图②中，结论：DP=DB．只要证明△DEP≌△DNB即可．

（3）结论：α+β=180°．只要证明∠1=∠3，即可解决问题．

解：(1)∵,，

∴,

∵，

∴,

∵，

∴△ABD是等边三角形，

∴,

∵,

∴,

∴

(2)结论：，理由如下：

证明：作于， 于．

∵，

∴

∵，

∴,,

∴，

∵

∴

∵

∴，

又∵

∴△DEP≌△DNB，

∴．

（3）结论：．

由（2）可知，

∵,

∴

∵

∴

∴

∵

∴

即．