题目内容
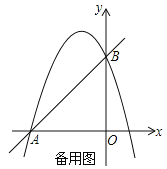
【题目】已知AB//CD，点C在点D的右侧，∠ABC，∠ADC的平分线交于点E(不与B，D点重合).
，
.
(1)若点B在点A的左侧，求∠BED的度数(用含
的代数式表示).
(2)将线段BC沿DC方向平移，当点B移动到点A右侧时，请画出图形并判断
的度数是否改变.若改变，请求出的度数(用含的代数式表示)；若不变，请说明理由.
【答案】(1)∠BED=
n°+40°；(2)
的度数改变，
或
.
【解析】
（1）过点E作
，根据平行线的性质推出
，
，根据角平分线的定义得出
，
，代入
可得．
（2）分类讨论，分点E在直线AB，CD之间时，点E在直线AB上方，点E在直线CD的下方三种情况，过点E作
，根据平行线的性质及角平分线的定义表达出角，代入即可．
(1)如图(1)，过点E作.
∵
，
∴
，
∴，.
∵BE平分
，DE平分
，
，
，
∴，，
∴
.
(2)的度数改变，或.
当点E在直线AB，CD之间时，过点E作，如图2.
∵BE平分，DE平分，，，
∴
，
∵，∴
，
∴
，
，
∴
当点E在直线AB上方时，如图(3)，
此时的平分线与的平分线BF的反向延长线相交于点E，
过点E作
.
同理得
，
.
∵，∴
，
∴
，
，
∴
.
当点E在直线CD的下方时，如图(4)，
此时的分线与∠ADC的平分线的反向延长线相交于点E，过E作
，
同理得
.
综上所述，的度数改变，或
练习册系列答案
相关题目
【题目】观察如图图形，把一个三角形分别连接其三边中点，构成4个小三角形，挖去中间的一个小三角形（如图1），对剩下的三个小三角形再分别重复以上做法，……，据此解答下面的问题
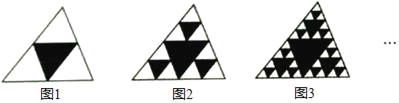
（1）填写下表：
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
（2）根据这个规律，求图n中挖去三角形的个数wn；（用含n的代数式表示）
（3）若图n+1中挖去三角形的个数为wn+1，求wn+1﹣Wn
