题目内容
5.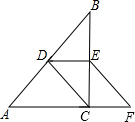 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,
如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,(1)CF=DE成立吗?试说明理由.
(2)若AC=6cm,AB=10cm,求四边形DCFE的面积.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半可得CD=BD,再根据等边对等角可得∠B=∠DCE,然后求出∠FEC=∠DCE,根据等腰三角形三线合一的性质可得∠CED=90°,然后求出∠CED=∠ECF=90°,再利用“角边角”证明△CDE和△ECF全等,根据全等三角形对应边相等证明即可.
(2)由三角形的中位线定理得到DE的长度,再由平行四边形的面积公式求得.
解答 解:(1)证明:∵∠ACB=90°,点D是AB的中点,
∴CD=BD,
∴∠B=∠DCE,
∵∠FEC=∠B,
∴∠FEC=∠DCE,
∵点E是BC的中点,
∴∠CED=90°,
∴∠CED=∠ECF=90°,
在△CDE和△ECF中,
$\left\{\begin{array}{l}{∠CED=∠ECF=90°}\\{CE=EC}\\{∠FEC=∠DCE}\end{array}\right.$
∴△CDE≌△ECF(ASA),
∴CF=DE;
(2)在Rt△ABC中,∠ACB=90°,
∴BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=8,
∵点D、E分别是AB、BC的中点,
∴DE=$\frac{1}{2}$AC=3,CE=$\frac{1}{2}BC=4$,
∴S四边形DCFE=3×4=12.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,全等三角形的判定与性质,熟记各性质并确定出全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图,图中共有线段的条数是( )
如图,图中共有线段的条数是( )
 如图,图中共有线段的条数是( )
如图,图中共有线段的条数是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7、 |
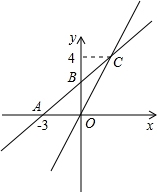 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=$\frac{4}{3}$x的图象交点为C(m,4).求:
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=$\frac{4}{3}$x的图象交点为C(m,4).求: