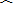题目内容
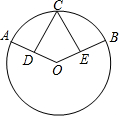
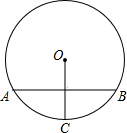
如图,⊙O的弦AB垂直平分半径OC,若AB=
,则⊙O的半径为( )
| 6 |
A.
| B.2
| C.
| D.
|

连接OA,设⊙O的半径为r,
∵AB垂直平分半径OC,AB=
,
∴AD=
=
,OD=
,
在Rt△AOD中,
OA2=OD2+AD2,即r2=(
)2+(
)2,
解得r=
.
故选A.

∵AB垂直平分半径OC,AB=
| 6 |
∴AD=
| AB |
| 2 |
| ||
| 2 |
| r |
| 2 |
在Rt△AOD中,
OA2=OD2+AD2,即r2=(
| r |
| 2 |
| ||
| 2 |
解得r=
| 2 |
故选A.


练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目