题目内容
【题目】已知抛物线![]() .
.
![]() 求该抛物线的对称轴和顶点P的坐标.
求该抛物线的对称轴和顶点P的坐标.
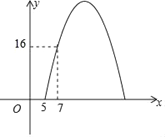
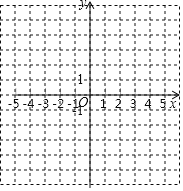
![]() 在图中的直角坐标系内用五点法画出该抛物线的图象.
在图中的直角坐标系内用五点法画出该抛物线的图象.
![]() 将该抛物线向下平移2个单位,向左平移3个单位得到抛物线
将该抛物线向下平移2个单位,向左平移3个单位得到抛物线![]() ,此时点P的对应点为
,此时点P的对应点为![]() ,试求直线
,试求直线![]() 与y轴的交点坐标.
与y轴的交点坐标.
【答案】![]() 对称轴为直线
对称轴为直线![]() ,顶点
,顶点![]() ;(2)见解析;
;(2)见解析;![]() y轴的交点为
y轴的交点为![]() 10
10![]() .
.
【解析】
(1)把抛物线解析式整理成顶点式解析式,然后写出对称轴和顶点坐标即可;
(2)令y=0,求出抛物线与x轴的交点坐标,令x=0,求出与y轴的交点,以及对称点,然后画出图象即可;
(3)根据顶点坐标的变化求得抛物线y1,得到顶点P′,然后求得直线PP′的解析式,令x=0,即可求得.
![]() ,
,
![]() 该抛物线的对称轴对称轴为直线
该抛物线的对称轴对称轴为直线![]() ,顶点
,顶点![]()
![]() 令
令![]() ,则
,则![]() ,解得
,解得![]() 或
或![]() ,
,
![]() 抛物线与x轴的交点为
抛物线与x轴的交点为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 抛物线与y轴的交点为
抛物线与y轴的交点为![]() ,
,
![]() 的对称点为
的对称点为![]() ,
,
函数的图象如图:

![]() 平移后抛物线为
平移后抛物线为![]()
![]()
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]()
![]()
即与y轴的交点为![]() 10
10![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目