题目内容
如图，以点O为圆心的两个同心圆，大圆的弦AB交小圆于C、D，如果AB=3cm，CD=2cm，那么AC= cm．
【答案】分析：根据题意：过O作OE⊥CD于E，根据垂径定理可以求出AE、CE的长度，AC的长度也就不难求出．
解答：
解：过O作OE⊥AB，垂足为E，
∵AB=3cm，CD=2cm，
∴AE=
AB=
×3=
cm，
CE=ED=
×2=1cm，
∴AC=AE-CE=
-1=
cm，
故答案为
．
点评：本题考查的是垂径定理，即垂直于弦的直径平分弦．
解答：
解：过O作OE⊥AB，垂足为E，∵AB=3cm，CD=2cm，
∴AE=
AB=×3=cm，CE=ED=
×2=1cm，∴AC=AE-CE=
-1=cm，故答案为
．点评：本题考查的是垂径定理，即垂直于弦的直径平分弦．
练习册系列答案
相关题目
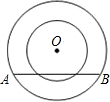如图，以点O为圆心的两个同心圆，半径分别为5和3，若大圆的弦AB与小圆相交，则弦长AB的取值范围是（ ）| A、8≤AB≤10 | B、AB≥8 | C、8＜AB≤10 | D、8＜AB＜10 |
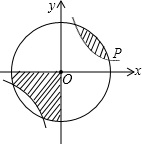如图，以点O为圆心的圆与反比例函数的图象相交，若其中一个交点P的坐标为（5，1），则图中两块阴影部分的面积和为
12、如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（4，2），点A的坐标为（2，0），则点B的坐标为
如图是以点O为圆心的半圆，AB是半圆的一条弦，延长OB与过点A的直线交于点C，AB=BC=OB．
如图，以点O为圆心的两个同心圆，当大圆的弦AB与小圆相切时弦长AB=8，则这两个同心圆所形成的圆环的面积是