题目内容
如图，点A在双曲线
上，点B在双曲线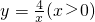
上，且AB∥y轴，点P是y轴上的任意一点，则△PAB的面积为________．
1
分析：设A（x，
），则B（x，
），再根据三角形的面积公式求解．
解答：设A（x，），
∵AB∥y轴，
∴B（x，），
∴S△ABP=
AB•x=（-）×x=1．
故答案为：1．
点评：本题考查的是反比例函数系数k的几何意义，先根据题意设出A点坐标，再由AB∥y轴得出B点坐标是解答此题的关键．
分析：设A（x，
），则B（x，），再根据三角形的面积公式求解．解答：设A（x，
），∵AB∥y轴，
∴B（x，
），∴S△ABP=
AB•x=（-）×x=1．故答案为：1．
点评：本题考查的是反比例函数系数k的几何意义，先根据题意设出A点坐标，再由AB∥y轴得出B点坐标是解答此题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
（2013•江阴市模拟）如图，点A在双曲线上，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于点B，当OA=4时，△ABC周长为
轴，垂足为
轴交于点F，已知AC：
上，且OA＝4，过A作AC⊥
轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为 ( ) 
B．5 C．
D．
上，AB⊥x轴于B，且△AOB的面积S△AOB=2，则k=______．