题目内容
某长途汽车客运公司规定旅客可随身携带一定质量的行李.如果超过规定质量,那么需要购买行李 票,行李票费用y(元)是行李质量x(kg)的一次函数.根据图象回答下列问题:
票,行李票费用y(元)是行李质量x(kg)的一次函数.根据图象回答下列问题:(1)求旅客最多可免费携带行李的质量;
(2)求y与x之间的函数关系式;
(3)某旅客所买的行李票的费用为4~15元,求他所带行李的质量的范围.
分析:(1)由图象可知,当行李费y=0时,行李质量x=10,由此可知可免费携带行李的质量;
(2)设一次函数y=kx+b,将(10,0),(40,6)代入可求函数关系式;
(3)根据(2)的函数关系式,列不等式组求x的取值范围.
(2)设一次函数y=kx+b,将(10,0),(40,6)代入可求函数关系式;
(3)根据(2)的函数关系式,列不等式组求x的取值范围.
解答:解:(1)观察图象得当y=0时,x=10,
∴1免费携带行李的质量为10千克;…(2分)
(2)设一次函数y=kx+b,将(10,0),(40,6)代入,
得
,
解得
,
∴y=
x-2; …(4分)
(3)依题意,得
…(5分)
解得30≤x≤85.…(6分)
答:旅客所带行李的质量的范围为30 kg到85kg.…(7分)
∴1免费携带行李的质量为10千克;…(2分)
(2)设一次函数y=kx+b,将(10,0),(40,6)代入,
得
|
解得
|
∴y=
| 1 |
| 5 |
(3)依题意,得
|
解得30≤x≤85.…(6分)
答:旅客所带行李的质量的范围为30 kg到85kg.…(7分)
点评:本题考查了一次函数的运用.关键是根据图象求一次函数解析式.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
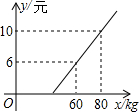 某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规这质量,则需购买行李费,如图是行李费y元是行李质量xkg的一次函数,那么旅客可携带的免费行李的最大质量为( )
某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规这质量,则需购买行李费,如图是行李费y元是行李质量xkg的一次函数,那么旅客可携带的免费行李的最大质量为( )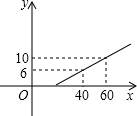 某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需要购买行李票.已知行李费y(元)是行李质量x(kg)之间的函数表达式为y=kx+b.这个函数的图象如图所示:
某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需要购买行李票.已知行李费y(元)是行李质量x(kg)之间的函数表达式为y=kx+b.这个函数的图象如图所示: