Question

【题目】定义：有一个内角为90°，且对角线相等的四边形称为“不完全矩形”.

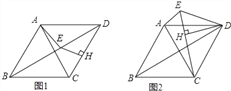
(1)①如图1，在不完全矩形中，，若，，则____；

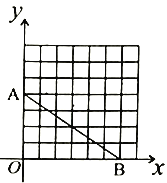
②如图2，在平面直角坐标系中，，，若整点使得四边形是不完全矩形，则点的坐标是_____；(整点指横坐标、纵坐标都为整数的点)

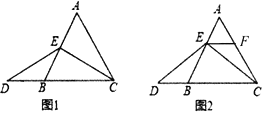
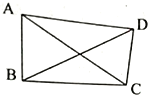
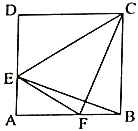
(2)如图3，在正方形中，点，分别是，上的点，且，求证：四边形是不完全矩形.

Answer 1

【答案】(1)①5；②(4，6)或(6，4)；(2)证明见解析.

【解析】

（1）①利用不完全矩形的定义和勾股定理计算；②利用不完全矩形的定义和勾股定理计算，再根据不完全矩形的特点和整点的特点求出即可；

（2）先利用正方形的性质判断出△ABE≌△BCF，即可证明四边形是不完全矩形.

(1) （1）①∵∠ABC=90，
∴BD=AC=，

故答案为5，

②∵A（0，4），B（6，0），

∴AB=，

设点P（m，n），

∴OP=AB=，

∵m，n都为整数，

∴点P(4，6)或(6，4)；

故答案为：P（(4，6)或(6，4)；

(2)证明：在正方形中，，.

∴，

∵，

∴.

∴，

∴，

∴，

∴四边形是不完全矩形.