Question

商场某种商品平均每天可销售40件，每件盈利60元．为减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价1元，商场平均每天可多销售2件．

（1）每件商品降价多少元时，商场日盈利可达到3150元？

（2）商场日盈利能否达到3300元？

（3）每件商品降价多少元时，商场日盈利最多？

Answer 1

【考点】一元二次方程的应用；二次函数的应用．

【分析】（1）根据日盈利=每件商品盈利的钱数×（原来每天销售的商品件数40+2×降价的钱数），把相关数值代入求解即可；

（2）根据日盈利=每件商品盈利的钱数×（原来每天销售的商品件数40+2×降价的钱数），整理后判断方程的根的情况即可；

（3）根据（1）得到的关系式判断出二次函数的对称轴，此时二次函数取到最值．

【解答】解：（1）设降价x元，由题意得：（60﹣x）（40+2x）=3150，

化简得：x²﹣40x+375=0，

解得：x₁=15，x₂=25，

∵该商场为了尽快减少库存，则x=15不合题意，舍去．∴x=25

答：每件商品降价25元，商场日盈利可达3150元；

（2）设降价x元，由题意得：（60﹣x）（40+2x）=3300，

化简得：x²﹣40x+450=0，

b²﹣4ac=1600﹣4×450=﹣200＜0，

故此方程无实数根，

故商场日盈利不能达到3300元；

（3）设利润为y元，根据题意可得：

y=（60﹣x）（40+2x）=﹣2x²+80x+2400，

当x=﹣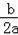=20时，y最大．

答：每件商品降价20元时，商场日盈利的最多．