Question

已知二次函数y=ax²+bx+c与x轴只有一个交点，且系数a、b满足条件：．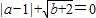
（1）求y=ax²+bx+c解析式；
（2）将y=ax²+bx+c向右平移一个单位，再向下平移一个单位得到函数y=mx²+nx+k，该函数交y轴于点C，交x轴于A、B（点A在点B的右侧），点P是该抛物线上一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．当△ADP是直角三角形时，求点P的坐标；
（3）在问题（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．

Answer 1

【答案】分析：（1）先根据非负数的性质求出a=1，b=-2，再由二次函数y=ax²+bx+c与x轴只有一个交点，得出一元二次方程ax²+bx+c=0有两个相等的实数根，则判别式△=0，从而求出c的值；
（2）先根据“上加下减，左加右减”的平移规律求出y=mx²+nx+k，再分情况讨论△ADP是直角三角形时，可能点P为直角顶点，也可能点A为直角顶点，①当点P₁为直角顶点时，点P₁与点B重合，将y=0代入抛物线的解析式，可求出点P的坐标；②当点A为直角顶点时，根据等腰三角形的性质得出P₂、D₂关于x轴对称，再由P₂在抛物线上，D₂在直线AC上可求出点P的坐标；
（3）由题（2）知，当点P的坐标为P₁（1，0）时，由于A、P、E三点都在抛物线上，所以不能构成平行四边形；当点P的坐标为抛物线的顶点Q时，平移直线AP交x轴于点E，交抛物线于点F，当AP=FE时，四边形PAFE是平行四边形，根据平行四边形的对角线互相平分可知对角线AE的中点与PF的中点重合，由P（2，-1）可设F（x，1），再根据点F在抛物线上列出关于x的方程，解方程即可．
解答：解：（1）∵，
∴a-1=0，b+2=0，
∴a=1，b=-2．
∵二次函数y=ax²+bx+c与x轴只有一个交点，
∴b²-4ac=0，即（-2）²-4×1×c=0，
解得c=1，
故所求抛物线的解析式为y=x²-2x+1；

（2）∵y=x²-2x+1=（x-1）²，
∴将y=（x-1）²向右平移一个单位，再向下平移一个单位得到函数y=（x-1-1）²-1，
即y=x²-4x+3．
当△ADP是直角三角形时，分两种情况：
①如果点P₁为直角顶点时，点P₁与点B重合，如图，
令y=0，得x²-4x+3=0，
解之得x₁=1，x₂=3，
∵点A在点B的右边，∴B（1，0），A（3，0），
∴P₁（1，0）；
②如果点A为直角顶点时，∠D₂AP₂=90°，如图，
∵OA=OC=3，∠AOC=90°，PD∥y轴，
∴∠AD₂P₂=∠ACO=45°，∠AP₂D₂=45°，
∴P₂、D₂关于x轴对称．
设直线AC的函数关系式为y=kx+b，
将A（3，0），C（0，3）代入上式，得
，
解得，
∴y=-x+3，
∵D₂在y=-x+3上，P₂在y=x²-4x+3上，
∴设D₂ （x，-x+3），P₂ （x，x²-4x+3），
∴（-x+3）+（x²-4x+3）=0，
整理，得x²-5x+6=0，
解得x₁=2，x₂=3（，不合题意，舍去），
∴当x=2时，x²-4x+3=4-8+3=-1，
∴P₂的坐标为P₂ （2，-1）（即为抛物线顶点），
∴P点坐标为P₁（1，0），P₂（2，-1）；

（3）在问题（2）的结论下，若点E在x轴上，点F在抛物线上，存在以A、P、E、F为顶点的平行四边形，此时点F的坐标为F₁（2-，1），F₂（2+，1），理由如下：
由题（2）知，当点P的坐标为P₁（1，0）时，不能构成平行四边形；
当点P的坐标为P₂（2，-1）时，平移直线AP （如图）交x轴于点E，交抛物线于点F，当AP=FE时，四边形PAFE是平行四边形，
∴AE与PF互相平分，对角线AE的中点与PF的中点重合，
∵P（2，-1），
∴可设F（x，1），
∴x²-4x+3=1，
解得x₁=2-，x₂=2+，
∴点F存在且坐标为F₁（2-，1），F₂（2+，1）．
点评：本题考查了二次函数的相关知识，是二次函数综合题，涉及到运用待定系数法求函数的解析式，解析式的平移规律，直角三角形、等腰三角形的性质，平行四边形的判定与性质以及存在性问题的基本思路，综合性较强，有一定难度．