题目内容
如图，在⊙O中，弦AB=6，⊙O的半径长为5，OC⊥AB于点D，交⊙O于点C，则CD=________．
1
分析：由OC⊥AB，根据垂径定理，即可得AD=BD=
AB=3，∠ADO=90°，然后在Rt△OAD中，利用勾股定理即可求得OD的长，则可得CD的长．
解答：∵OC⊥AB，
∴AD=BD=AB=×6=3，∠ADO=90°，
∵OA=5，
在Rt△OAD中，OD=
=4，
∴CD=OC-OD=5-4=1．
故答案为：1．
点评：此题考查了垂径定理与勾股定理的应用．此题难度不大，解题的关键是注意数形结合思想的应用．
分析：由OC⊥AB，根据垂径定理，即可得AD=BD=
AB=3，∠ADO=90°，然后在Rt△OAD中，利用勾股定理即可求得OD的长，则可得CD的长．解答：∵OC⊥AB，
∴AD=BD=
AB=×6=3，∠ADO=90°，∵OA=5，
在Rt△OAD中，OD=
=4，∴CD=OC-OD=5-4=1．
故答案为：1．
点评：此题考查了垂径定理与勾股定理的应用．此题难度不大，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
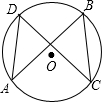已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．
4、如图，在⊙O中，弦BC∥半径OA，AC与OB相交于M，∠C=20°，则∠AMB的度数为（ ）
标系．
如图，在⊙O中，弦AB=BC=CD，且∠ABC=140°，则∠AED=（ ）
如图，在⊙O中，弦AB与CD相交于点P，连接AC、DB．