Question

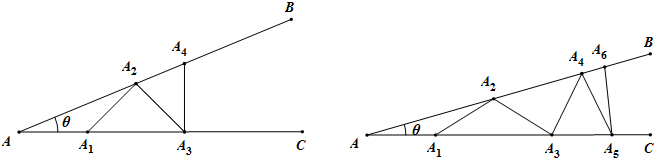
某数学兴趣小组开展了一次课外活动，过程如下：如图1，正方形ABCD中，AB=6，将三角板放在正方形ABCD上，使三角板的直角顶点与D点重合．三角板的一边交AB于点P，另一边交BC的延长线于点Q．

（1）求证：DP=DQ；

（2）如图2，小明在图1的基础上作∠PDQ的平分线DE交BC于点E，连接PE，他发现PE和QE存在一定的数量关系，请猜测他的结论并予以证明；

（3）如图3，固定三角板直角顶点在D点不动，转动三角板，使三角板的一边交AB的延长线于点P，另一边交BC的延长线于点Q，仍作∠PDQ的平分线DE交BC延长线于点E，连接PE，若AB：AP=3：4，请帮小明算出△DEP的面积．

 

 

Answer 1

【答案】

（1）详见试题解析;（2）详见试题解析;（3）

【解析】

试题分析：

（1）证明△ADP≌△CDQ，即可得到结论：DP=DQ；

（2）证明△DEP≌△DEQ，即可得到结论：PE=QE；

（3）与（1）（2）同理，可以分别证明△ADP≌△CDQ、△DEP≌△DEQ．在Rt△BPE中，利用勾股定理求出PE（或QE）的长度，从而可求得S_△DEQ=，而△DEP≌△DEQ，所以S_△DEP=S_△DEQ=．

试题解析：（1）证明：∵∠ADC=∠PDQ=90°

∴∠ADP=∠CDQ

∠DAP＝∠DCQ＝90°  AD＝CD

∴△ADP≌△CDQ（ASA）

∴DP=DQ                                （4分）

（2）猜测：PE=QE                    （5分）

由（1）可知，DP=DQ

∠PDE＝∠QDE＝45°  DE＝DE

∴△DEP≌△DEQ（SAS）

∴PE=QE                             （8分）

（3）∵AB:AP=3:4，AB=6

∴AP=8，BP=2

与（1）同理，可以证明△ADP≌△CDQ

∴CQ=AP=8

与（2）同理，可以证明△DEP≌△DEQ

∴PE=QE

设QE=PE=x，则BE=BC+CQ-QE=14-x

在Rt△BPE中，由勾股定理得：BP²+BE²=PE²

即：2²+（14-x）²=x²，

解得：x=  即QE=

∴S_△DEQ=××6=

∵△DEP≌△DEQ

∴S_△DEP=S_△DEQ=                （12分）

考点：四边形综合题．