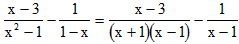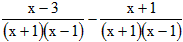题目内容
先化简，再求值：
，其中a、b满足（a-2）2+|b+1|=0．
解：原式=3ab2-4ab2+2a2b-2a2b+5ab2，
=4ab2，
∵（a-2）2+|b+1|=0，
∴a=2，b=-1，
∴原式=4×2×（-1）2
=8．
分析：首先去掉多项式的括号，然后合并同类项，再利用非负数的性质可以求出a、b的值，代入化简后的多项式中即可解决问题．
点评：此题考查了多项式的化简求值，也利用了非负数的性质确定字母的取值．
=4ab2，
∵（a-2）2+|b+1|=0，
∴a=2，b=-1，
∴原式=4×2×（-1）2
=8．
分析：首先去掉多项式的括号，然后合并同类项，再利用非负数的性质可以求出a、b的值，代入化简后的多项式中即可解决问题．
点评：此题考查了多项式的化简求值，也利用了非负数的性质确定字母的取值．
练习册系列答案
相关题目
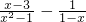，其x=2”某同学写出了如下解答：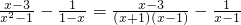
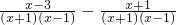
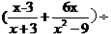
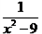，其中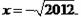
小张同学做题时把“
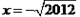”错写成了“
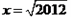”，但他的计算结果也是正确的，请你解释这是怎么回事？
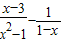，其x=2”某同学写出了如下解答：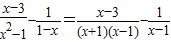
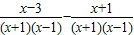
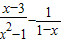，其x=2”某同学写出了如下解答：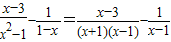
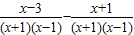
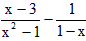，其x=2”某同学写出了如下解答：
