题目内容
四边形ABCD中,BD平分∠ABC,且DA=DC,请你选用恰当的工具画图说明∠A与∠C的数量关系是________.
相等或互补
分析:画出符合题意的两种情况的图形,①当AB=BC时,证△ABD≌△CBD,即可求出答案,②当AB≠BC时,在BC上截取BC′=AB,连接DC′,证△ABD≌△C′BD,推出∠A=∠BC′D,即可求出答案.
解答: 解:如图1,当AB=BC时,
解:如图1,当AB=BC时,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵在△ABD和△CBD中
 ,
,
∴△ABD≌△CBD(SAS),
∴∠A=∠C;
如图2,当AB≠BC时,在BC上截取BC′=AB,连接DC′,
同理求出△ABD≌△C′BD,
∴∠A=∠DC′B,AD=DC′,
∵AD=DC,
∴DC′=DC,
∴∠C=∠DC′C,
∵∠DC′B+′DC′C=180°,
∴∠A+∠C=180°,
即∠A和∠C的关系式相等或互补.
故答案为:相等或互补.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.
分析:画出符合题意的两种情况的图形,①当AB=BC时,证△ABD≌△CBD,即可求出答案,②当AB≠BC时,在BC上截取BC′=AB,连接DC′,证△ABD≌△C′BD,推出∠A=∠BC′D,即可求出答案.
解答:
 解:如图1,当AB=BC时,
解:如图1,当AB=BC时,∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵在△ABD和△CBD中
 ,
,∴△ABD≌△CBD(SAS),
∴∠A=∠C;
如图2,当AB≠BC时,在BC上截取BC′=AB,连接DC′,
同理求出△ABD≌△C′BD,
∴∠A=∠DC′B,AD=DC′,
∵AD=DC,
∴DC′=DC,
∴∠C=∠DC′C,
∵∠DC′B+′DC′C=180°,
∴∠A+∠C=180°,
即∠A和∠C的关系式相等或互补.
故答案为:相等或互补.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.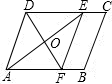 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.