Question

【题目】如图，等边三角形ABC的边长为4厘米，长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动（运动开始时，点M与点A重合，点N到达点B时运动终止），过点M、N分别作AB边的垂线，与△ABC的其它边交于P、Q两点．线段MN在运动的过程中，四边形MNQP的面积为S，运动的时间为t．则大致反映S与t变化关系的图象是（ ）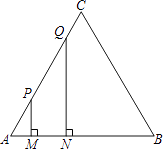

A.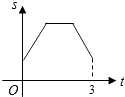
B.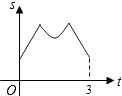
C.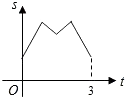
D.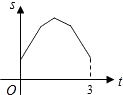

Answer 1

【答案】A
【解析】解：过点C作CG⊥AB，

∵MN=1，四边形MNQP为直角梯形，

∴四边形MNQP的面积为S= MN×（PM+QN），

∴N点从A到G点四边形MNQP的面积为S= MN×（PM+QN）中，PM，QN都在增大，所以面积也增大；

当QN=CG时，QN开始减小，但PM仍然增大，且PM+QN不变，

∴四边形MNQP的面积不发生变化，

当PM＜CG时，PM+QN开始减小，

∴四边形MNQP的面积减小，

∴符合要求的只有A．

所以答案是：A．

【考点精析】掌握直角梯形是解答本题的根本，需要知道一腰垂直于底的梯形是直角梯形．