题目内容
 如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点M
如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点M
(1)直线FC与O有何位置关系?并说明理由;
(2)若OB=BM,CM=2 ,求⊙O的半径.
,求⊙O的半径.
 (1)答:直线FC与⊙O相切;
(1)答:直线FC与⊙O相切;证明:连接OC,
∵直径AB垂直于弦CD,
∵将△ACE沿AC翻折得到△ACF,
∴∠F=∠CEA=90°,∠FAC=∠EAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠FAC=∠OCA,
∴OC∥AF,
∴OC⊥FG,
∴直线FC与⊙O相切;
(2)解:由(1)知,△COM为直角三角形,连接CB,
∵OB=BM,
∴CB=OB=BM,
∴∠COM=60°,
在Rt△COM中,设OC=x,则OM=2x,
由勾股定理得:OM2-OC2=CM2,
即(2x)2-x2=(2
 )2,
)2,解得:x=2,
答:⊙O的半径为2.
分析:(1)连接OC,通过证明OC∥AF,从而证得OC⊥FG即可判定切线.
(2)首先根据题意得出∠COM=60°,进而利用勾股定理求得⊙O的半径的长即可.
点评:本题考查了切线的性质和判定,平行线的性质,等腰三角形性质,垂径定理,解直角三角形等知识点的应用,能综合运用这些性质进行推理是解此题的关键,题型较好.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
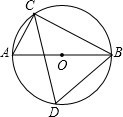 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=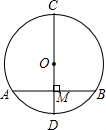 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.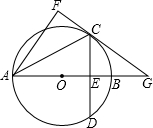 C与直线AB相交于点G.
C与直线AB相交于点G. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )