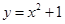题目内容
如图,点P是直线 上的一个动点,过点P作PA⊥x轴,垂足为A,请问:y轴上是否存在一点B,使得△PAB为等腰直角三角形。小明发现,点P坐标为(2,2)时,y轴上存在B(0,2),使得△PAB为等腰直角三角形。请写出其它点P的坐标
上的一个动点,过点P作PA⊥x轴,垂足为A,请问:y轴上是否存在一点B,使得△PAB为等腰直角三角形。小明发现,点P坐标为(2,2)时,y轴上存在B(0,2),使得△PAB为等腰直角三角形。请写出其它点P的坐标 
 上的一个动点,过点P作PA⊥x轴,垂足为A,请问:y轴上是否存在一点B,使得△PAB为等腰直角三角形。小明发现,点P坐标为(2,2)时,y轴上存在B(0,2),使得△PAB为等腰直角三角形。请写出其它点P的坐标
上的一个动点,过点P作PA⊥x轴,垂足为A,请问:y轴上是否存在一点B,使得△PAB为等腰直角三角形。小明发现,点P坐标为(2,2)时,y轴上存在B(0,2),使得△PAB为等腰直角三角形。请写出其它点P的坐标 

试题分析:若PA为斜边时,则∠OAB=45°,所以OA=OB,设点P(x,-2x+6),则A点坐标为(x,0)、B点坐标为(0,x),AB长为
 x,而AP的长为-2x+6,∵AP=
x,而AP的长为-2x+6,∵AP= AB,∴-2x+6=2x,解得x=
AB,∴-2x+6=2x,解得x= ,代入直线方程得出P点坐标为(
,代入直线方程得出P点坐标为( ,3);又当P运动到第四象限时,要PA=PB,且PA⊥PB,设点P(x,-2x+6),则有-x=-2x+6,解得x=6,所以点P坐标为(6,-6).故本题答案为:
,3);又当P运动到第四象限时,要PA=PB,且PA⊥PB,设点P(x,-2x+6),则有-x=-2x+6,解得x=6,所以点P坐标为(6,-6).故本题答案为: .
.点评:本题主要采用分类讨论法,来求得符合条件的点P坐标.

练习册系列答案
相关题目

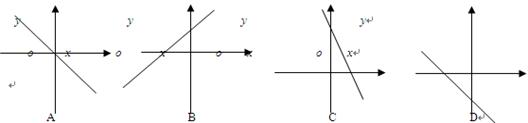
 (m-2)
(m-2)
 与x轴、y轴围成一个三角形,则这个三角形面积为___________.
与x轴、y轴围成一个三角形,则这个三角形面积为___________.