题目内容
如图,⊙O1与⊙O2相交于A、B两点,AC为⊙O1的直径,CA、CB的延长线分别交⊙O2于点D、E, AC=6cm,BE=11cm,AD=BC.求:
AC=6cm,BE=11cm,AD=BC.求:(1)BC的长;
(2)∠DEC的余弦值;
(3)两圆⊙O1和⊙O2的圆心距.
分析:(1)已知了AC、BE的长,可直接由切割线定理求出BC的长;
(2)连接AB;此时四边形ABED是⊙O2的内接四边形,则∠CAB=∠E,因此只需在Rt△ABC中求得∠BAC的余弦值即可.
(3)连接AE,易知∠ABE=90°,由圆周角定理可得AE是⊙O2的直径,那么O1O2即为△ACE的中位线,在(1)中求得了BC的长,即可得到EC的长,根据三角形中位线定理即可求出两圆的圆心距.
(2)连接AB;此时四边形ABED是⊙O2的内接四边形,则∠CAB=∠E,因此只需在Rt△ABC中求得∠BAC的余弦值即可.
(3)连接AE,易知∠ABE=90°,由圆周角定理可得AE是⊙O2的直径,那么O1O2即为△ACE的中位线,在(1)中求得了BC的长,即可得到EC的长,根据三角形中位线定理即可求出两圆的圆心距.
解答: 解:(1)设BC=xcm,则AD=xcm,由切割线定理的推论知CA•CD=CB•CE;
解:(1)设BC=xcm,则AD=xcm,由切割线定理的推论知CA•CD=CB•CE;
6(6+x)=x(x+11),(1分)
即x2+5x-36=0,解得x1=4,x2=-9(舍去)
∴BC=4cm;(2分)
(2)连接AB;∵AC是⊙O1的直径,
∴CB⊥AB;
∴AB=
=
=2
;(4分)
又∵四边形ABED是圆内接四边形,
∴∠CAB=∠DEC,
∴cos∠DEC=cos∠CAB=
=
=
;(4分)
(3)连接AE;∵AB⊥BC,
∴∠ABE=90°;
∴AE是⊙O2的直径,O1,O2分别为AC、AE的中点.
∴O1O2=
CE=
(4+11)=
(cm).(6分)
 解:(1)设BC=xcm,则AD=xcm,由切割线定理的推论知CA•CD=CB•CE;
解:(1)设BC=xcm,则AD=xcm,由切割线定理的推论知CA•CD=CB•CE;6(6+x)=x(x+11),(1分)
即x2+5x-36=0,解得x1=4,x2=-9(舍去)
∴BC=4cm;(2分)
(2)连接AB;∵AC是⊙O1的直径,
∴CB⊥AB;
∴AB=
| AC2-BC2 |
| 62-42 |
| 5 |
又∵四边形ABED是圆内接四边形,
∴∠CAB=∠DEC,
∴cos∠DEC=cos∠CAB=
| AB |
| AC |
2
| ||
| 6 |
| ||
| 3 |
(3)连接AE;∵AB⊥BC,
∴∠ABE=90°;
∴AE是⊙O2的直径,O1,O2分别为AC、AE的中点.
∴O1O2=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
点评:此题主要考查了圆周角定理、切割线定理、圆内接四边形的性质、三角形中位线定理以及解直角三角形的应用等知识.

练习册系列答案
相关题目
 12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=
12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=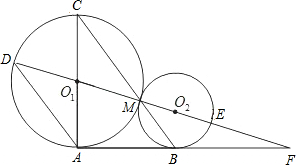 已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.
已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.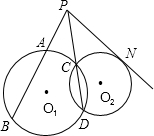 如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN=
如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN=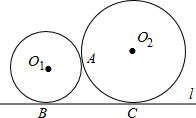 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.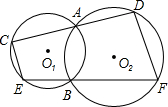 已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.
已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.