题目内容
 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试说明:AD平分∠BAC.
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试说明:AD平分∠BAC.
答:∵AD⊥BC,EG⊥BC
∴AD∥EG(________)
∴∠1=∠E(________)
∠2=∠3(________ )
又∵∠3=∠E
∴∠1=∠2
∴AD平分∠BAC(________)
同垂直于一条直线的两直线平行 两直线平行,同位角相等 两直线平行,内错角相等 角平分线定义
分析:先由AD⊥BC,EG⊥BC推出AD∥EG,相继推出∠1=∠E,∠2=∠3,等量代换得∠1=∠2,所以得出AD平分∠BAC.
解答:∵AD⊥BC,EG⊥BC
∴AD∥EG(同垂直于一条直线的两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(两直线平行,内错角相等)
又∵∠3=∠E
∴∠1=∠2
∴AD平分∠BAC(角平分线定义)
故答案分别为:同垂直于一条直线的两直线平行,两直线平行、同位角相等,两直线平行、内错角相等,角平分线定义.
点评:此题考查的知识点是平行线的判定与性质,解题的关键是先判定AD∥EG,再由平行线的性质加上等量代换推出∠1=∠2.即AD平分∠BAC.
分析:先由AD⊥BC,EG⊥BC推出AD∥EG,相继推出∠1=∠E,∠2=∠3,等量代换得∠1=∠2,所以得出AD平分∠BAC.
解答:∵AD⊥BC,EG⊥BC
∴AD∥EG(同垂直于一条直线的两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(两直线平行,内错角相等)
又∵∠3=∠E
∴∠1=∠2
∴AD平分∠BAC(角平分线定义)
故答案分别为:同垂直于一条直线的两直线平行,两直线平行、同位角相等,两直线平行、内错角相等,角平分线定义.
点评:此题考查的知识点是平行线的判定与性质,解题的关键是先判定AD∥EG,再由平行线的性质加上等量代换推出∠1=∠2.即AD平分∠BAC.

练习册系列答案
相关题目
 15、如图,AD⊥BC于D,DE∥AC,则∠C与∠ADE之和为
15、如图,AD⊥BC于D,DE∥AC,则∠C与∠ADE之和为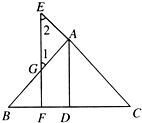 23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2. 22、如图,AD⊥BC于D,EF⊥BC于F,且∠E=∠1,求证∠BAD=∠CAD.
22、如图,AD⊥BC于D,EF⊥BC于F,且∠E=∠1,求证∠BAD=∠CAD. 23、如图,AD⊥BC于D,EF⊥BC于E,∠1=∠2,AB与DG平行吗?为什么?
23、如图,AD⊥BC于D,EF⊥BC于E,∠1=∠2,AB与DG平行吗?为什么? (2013•义乌市)如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC=
(2013•义乌市)如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC=