ÌâÄżÄÚÈĘ
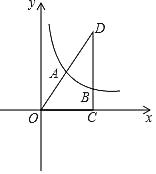
ĄŸÌâÄżĄżÒŃÖȘĆŚÎïÏßyŁœax2+bx+2ŸčęAŁš©1ŁŹ0Ł©ŁŹBŁš2ŁŹ0Ł©ŁŹCÈę”㣟ֱÏßyŁœmx+![]() œ»ĆŚÎïÏßÓÚAŁŹQÁœ”㣏”ăPÊÇĆŚÎïÏßÉÏÖ±ÏßAQÉÏ·œ”ÄÒ»žö¶Ż”㣏ŚśPFĄÍxÖᣏŽčŚăÎȘFŁŹœ»AQÓÚ”ăNŁź
œ»ĆŚÎïÏßÓÚAŁŹQÁœ”㣏”ăPÊÇĆŚÎïÏßÉÏÖ±ÏßAQÉÏ·œ”ÄÒ»žö¶Ż”㣏ŚśPFĄÍxÖᣏŽčŚăÎȘFŁŹœ»AQÓÚ”ăNŁź

Łš1Ł©ÇóĆŚÎïÏߔĜâÎöÊœŁ»
Łš2Ł©ÈçÍŒąÙŁŹ”±”ăPÔ˶Ż”œÊČÎλÖĂʱŁŹÏ߶ÎPNŁœ2NFŁŹÇółöŽËʱ”ăP”ÄŚű±êŁ»
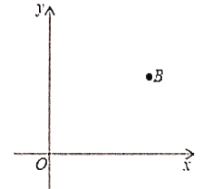
Łš3Ł©ÈçÍŒąÚŁŹÏ߶ÎAC”ÄŽčֱƜ·ÖÏßœ»xÖáÓÚ”ăEŁŹŽčŚăÎȘDŁŹ”ăMÎȘĆŚÎïÏߔĶ„”㣏ÔÚÖ±ÏßDEÉÏÊÇ·ńŽæÔÚÒ»”ăGŁŹÊ襜CMG”ÄÖÜł€ŚîĐĄŁżÈôŽæÔÚŁŹÇëÇółö”ăG”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
ĄŸŽđ°žĄżŁš1Ł©yŁœ©x2+x+2Ł»Łš2Ł©”ăP”ÄŚű±êÎȘŁš![]() ŁŹ
ŁŹ![]() Ł©Ł»Łš3Ł©ÔÚÖ±ÏßDEÉÏŽæÔÚÒ»”ăGŁŹÊ襜CMG”ÄÖÜł€ŚîĐĄŁŹŽËʱGŁš©
Ł©Ł»Łš3Ł©ÔÚÖ±ÏßDEÉÏŽæÔÚÒ»”ăGŁŹÊ襜CMG”ÄÖÜł€ŚîĐĄŁŹŽËʱGŁš©![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź
ĄŸœâÎöĄż
Łš1Ł©œ«”ăAșÍ”ăB”ÄŚű±êŽúÈëĆŚÎïÏߔĜâÎöÊœ”Ă”œčŰÓÚbĄąc”Ä·œłÌŚéŁŹÈ»șóÇó”ĂaŁŹb”ÄÖ”ŁŹŽÓ¶ű”Ă”œÎÊÌâ”Ď𰞣»
Łš2Ł©°ŃAŁš©1ŁŹ0Ł©ŽúÈëyŁœmx+![]() Çó”Ăm”ÄÖ”ŁŹżÉ”Ă”œÖ±ÏßAQ”ÄœâÎöÊœŁŹÉè”ăP”ÄșáŚű±êÎȘnŁŹÔòPŁšnŁŹ©n2+n+2Ł©ŁŹNŁšnŁŹ
Çó”Ăm”ÄÖ”ŁŹżÉ”Ă”œÖ±ÏßAQ”ÄœâÎöÊœŁŹÉè”ăP”ÄșáŚű±êÎȘnŁŹÔòPŁšnŁŹ©n2+n+2Ł©ŁŹNŁšnŁŹ![]() n+
n+![]() Ł©ŁŹFŁšnŁŹ0Ł©ŁŹ
Ł©ŁŹFŁšnŁŹ0Ł©ŁŹ
È»șóÓĂșŹn”ÄÊœŚÓ±íÊŸłöPNĄąNF”Äł€ŁŹÈ»șóÒÀŸĘPNŁœ2NFÁĐ·œłÌÇóœâŒŽżÉŁ»
Łš3Ł©ÁŹœáAMœ»Ö±ÏßDEÓë”ăGŁŹÁŹœáCGĄąCMŽËʱŁŹĄśCMG”ÄÖÜł€ŚîĐĄŁŹÏÈÇó”Ă”ăM”ÄŚű±êŁŹÈ»șóÇó”ĂAMșÍDE”ÄœâÎöÊœŁŹŚîșóÔÚÇó”ĂÁœÖ±ÏߔĜ»”ăŚű±êŒŽżÉŁź
Łš1Ł©ĄßĆŚÎïÏßyŁœax2+bx+2ŸčęAŁš©1ŁŹ0Ł©ŁŹBŁš2ŁŹ0Ł©ŁŹ
Ąàœ«”ăAșÍ”ăB”ÄŚű±êŽúÈë”ĂŁș![]() ŁŹœâ”ĂaŁœ©1ŁŹbŁœ1ŁŹ
ŁŹœâ”ĂaŁœ©1ŁŹbŁœ1ŁŹ
ĄàĆŚÎïÏߔĜâÎöÊœÎȘyŁœ©x2+x+2Łź
Łš2Ł©Ö±ÏßyŁœmx+![]() œ»ĆŚÎïÏßÓëAĄąQÁœ”㣏°ŃAŁš©1ŁŹ0Ł©ŽúÈëœâÎöÊœ”ĂŁșmŁœ
œ»ĆŚÎïÏßÓëAĄąQÁœ”㣏°ŃAŁš©1ŁŹ0Ł©ŽúÈëœâÎöÊœ”ĂŁșmŁœ![]() ŁŹ
ŁŹ
ĄàÖ±ÏßAQ”ÄœâÎöÊœÎȘyŁœ![]() x+
x+![]() Łź
Łź
Éè”ăP”ÄșáŚű±êÎȘnŁŹÔòPŁšnŁŹ©n2+n+2Ł©ŁŹNŁšnŁŹ![]() n+
n+![]() Ł©ŁŹFŁšnŁŹ0Ł©ŁŹ
Ł©ŁŹFŁšnŁŹ0Ł©ŁŹ
ĄàPNŁœ©n2+n+2©Łš![]() n+
n+![]() Ł©Łœ©n2+
Ł©Łœ©n2+![]() n+
n+![]() ŁŹNFŁœ
ŁŹNFŁœ![]() n+
n+![]() Łź
Łź
ĄßPNŁœ2NFŁŹŒŽ©n2+![]() n+
n+![]() Łœ2ĄÁŁš
Łœ2ĄÁŁš![]() n+
n+![]() Ł©ŁŹœâ”ĂŁșnŁœ©1»ò
Ł©ŁŹœâ”ĂŁșnŁœ©1»ò![]() Łź
Łź
”±nŁœ©1ʱŁŹ”ăPÓë”ăAÖŰșÏŁŹČ»·ûșÏÌâÒâÉáÈ„Łź
Ąà”ăP”ÄŚű±êÎȘŁš![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź
Łš3Ł©ĄßyŁœ©x2+x+2ŁŹŁœ©Łšx©![]() Ł©2+
Ł©2+![]() ŁŹ
ŁŹ
ĄàMŁš![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź
ÈçÍŒËùÊŸŁŹÁŹœáAMœ»Ö±ÏßDEÓë”ăGŁŹÁŹœáCGĄąCMŽËʱŁŹĄśCMG”ÄÖÜł€ŚîĐĄŁź

ÉèÖ±ÏßAM”ÄșŻÊęœâÎöÊœÎȘyŁœkx+bŁŹÇÒčęAŁš©1ŁŹ0Ł©ŁŹMŁš![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź
žùŸĘÌâÒâ”ĂŁș ŁŹœâ”Ă
ŁŹœâ”Ă![]() Łź
Łź
ĄàÖ±ÏßAM”ÄșŻÊęœâÎöÊœÎȘyŁœ![]() x+
x+![]() Łź
Łź
ĄßDÎȘAC”ÄÖД㣏
ĄàDŁš©![]() ŁŹ1Ł©Łź
ŁŹ1Ł©Łź
ÉèÖ±ÏßAC”ÄœâÎöÊœÎȘyŁœkx+2ŁŹœ«”ăA”ÄŚű±êŽúÈë”ĂŁș©k+2Łœ0ŁŹœâ”ĂkŁœ2ŁŹ
ĄàAC”ÄœâÎöÊœÎȘyŁœ2x+2Łź
ÉèÖ±ÏßDE”ÄœâÎöÊœÎȘyŁœ©![]() x+cŁŹœ«”ăD”ÄŚű±êŽúÈë”ĂŁș
x+cŁŹœ«”ăD”ÄŚű±êŽúÈë”ĂŁș![]() +cŁœ1ŁŹœâ”ĂcŁœ
+cŁœ1ŁŹœâ”ĂcŁœ![]() ŁŹ
ŁŹ
ĄàÖ±ÏßDE”ÄœâÎöÊœÎȘyŁœ©![]() x+
x+![]() Łź
Łź
œ«yŁœ©![]() x+
x+![]() ÓëyŁœ
ÓëyŁœ![]() x+
x+![]() ÁȘÁąŁŹœâ”ĂŁșxŁœ©
ÁȘÁąŁŹœâ”ĂŁșxŁœ©![]() ŁŹyŁœ
ŁŹyŁœ![]() Łź
Łź
ĄàÔÚÖ±ÏßDEÉÏŽæÔÚÒ»”ăGŁŹÊ襜CMG”ÄÖÜł€ŚîĐĄŁŹŽËʱGŁš©![]() ŁŹ
ŁŹ![]() Ł©Łź
Ł©Łź

 ÔőŃùѧșĂĆŁœòÓąÓïÏ”ÁĐŽđ°ž
ÔőŃùѧșĂĆŁœòÓąÓïÏ”ÁĐŽđ°ž ”ŒŃ§œÌłÌžßÖĐĐ¿αêÏ”ÁĐŽđ°ž
”ŒŃ§œÌłÌžßÖĐĐ¿αêÏ”ÁЎ𰞥ŸÌâÄżĄż¶ĄÀÏÊŠÎȘÁËœâËùÈΜ̔ÄÁœžö°à”ÄѧÉúÊęŃ§Ń§Ï°ÇéżöŁŹ¶ÔÊęѧœűĐĐÁËÒ»ŽÎČâÊÔŁŹ»ń”ĂÁËÁœžö°à”ÄłÉŒšŁš°Ù·ÖÖÆŁ©ŁŹČą¶ÔÊęŸĘŁšłÉŒšŁ©œűĐĐŐûÀíĄąĂèÊöșÍ·ÖÎöŁŹÏÂĂæžűłöÁËČż·ÖĐĆÏąŁź
ąÙAĄąBÁœ°àѧÉúŁšÁœžö°à”ÄÈËÊęÏàÍŹŁ©ÊęѧłÉŒšČ»ÍêŐû”ÄÆ”Êę·ÖČŒÖ±·œÍŒÈçÏÂŁšÊęŸĘ·ÖłÉ5ŚéŁșx<60ŁŹ60ĄÜx<70ŁŹ70ĄÜx<80ŁŹ80ĄÜx<90ŁŹ90ĄÜxĄÜ100Ł©Łș
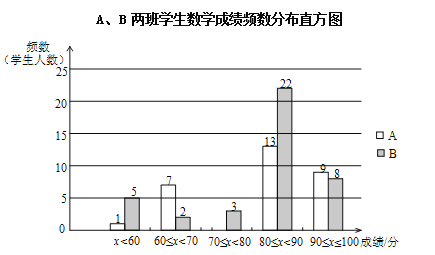
ąÚAĄąBÁœ°àѧÉúČâÊÔłÉŒšÔÚ80ĄÜx<90ŐâÒ»Śé”ÄÊęŸĘÈçÏÂŁș
A°àŁș80 80 82 83 85 85 86 87 87 87 88 89 89
B°àŁș80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
ąÛAĄąBÁœ°àѧÉúČâÊÔłÉŒš”ÄÆœŸùÊꥹÖĐλÊꥹ·œČîÈçÏÂŁș
ÆœŸùÊę | ÖĐλÊę | ·œČî | |
A°à | 80.6 | m | 96.9 |
B°à | 80.8 | n | 153.3 |
žùŸĘÒÔÉÏĐĆÏąŁŹ»ŰŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©ČčÈ«ÊęѧłÉŒšÆ”Êę·ÖČŒÖ±·œÍŒŁ»
Łš2Ł©ĐŽłö±íÖĐmĄąn”ÄÖ”Ł»
Łš3Ł©ÇëÄă¶Ô±È·ÖÎöAĄąBÁœ°àѧÉú”ÄÊęŃ§Ń§Ï°ÇéżöŁšÖÁÉÙŽÓÁœžöȻ͏”ĜǶȷÖÎöŁ©Łź