题目内容
如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
(1)证明:∵ABCD是正方形
∴AD=BC,∠ADC=∠BCD=90°
又∵△CDE是等边三角形
∴CE=CD,∠EDC=∠ECD=60°
∴∠ADE=∠ECB
∴△ADE≌△BCE(SAS)
(2)∠AFB=75°
解析试题分析:(1)由题意正方形ABCD的边AD=BC,在等边三角形CDE中,CE=DE,
∠EDC等于∠ECD,即能证其全等,如下:
证明:∵ABCD是正方形
∴AD=BC,∠ADC=∠BCD=90°
又∵△CDE是等边三角形
∴CE=CD,∠EDC=∠ECD=60°
∴∠ADE=∠ECB
∴△ADE≌△BCE(SAS)
(2)根据等边三角形、等腰三角形、平行线的角度关系,即可求得∠AFB的度数,如下
解:∵△CDE是等边三角形
∴CE=CD=DE
∵四边形ABCD是正方形
∴CD=BC
∴CE=BC
∴△CBE为等腰三角形,且顶角∠ECB=90°﹣60°=30°
∴∠EBC= (180°﹣30°)=75°
(180°﹣30°)=75°
∵AD∥BC
∴∠AFB=∠EBC=75°
考点:正方形的性质,等腰三角形,等边三角形的性质,全等三角形的判定
点评:本题属于几何的基础题目,综合考虑正方形、等腰三角形、等边三角形的性质,掌握两个三角形全等的判定。

练习册系列答案
相关题目
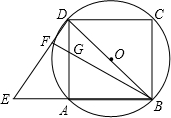 如图,点E是正方形ABCD边BA延长线上一点(AE<AD),连接DE.与正方形ABCD的外接圆相交于点F,BF与AD相交于点G.
如图,点E是正方形ABCD边BA延长线上一点(AE<AD),连接DE.与正方形ABCD的外接圆相交于点F,BF与AD相交于点G. (2013•包头)如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=
(2013•包头)如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= 如图,点E是正方形ABCD边BC的中点,H是BC延长线上的一点,EG⊥AE于点E,交边CD于G,
如图,点E是正方形ABCD边BC的中点,H是BC延长线上的一点,EG⊥AE于点E,交边CD于G, (2013•青铜峡市模拟)如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA.
(2013•青铜峡市模拟)如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA. 如图,点M是正方形ABCD的边CD的中点,正方形ABCD的边长为4cm,点P按A-B-C-M-D的顺序在正方形的边上以每秒1cm的速度作匀速运动,设点P的运动时间为x(秒),△APM的面积为y(cm2)
如图,点M是正方形ABCD的边CD的中点,正方形ABCD的边长为4cm,点P按A-B-C-M-D的顺序在正方形的边上以每秒1cm的速度作匀速运动,设点P的运动时间为x(秒),△APM的面积为y(cm2)