题目内容
如图,已知△ABC是面积为 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
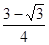
解析试题分析:先根据AB=2AD,△ABC∽△ADE,△ABC是面积为 求出△ADE的面积,再判断出△ADE的形状,根据等边三角形的面积求出AE的长,作FG⊥AE于G,由等边三角形及直角三角形的性质判断出△AFG是等腰直角三角形,设AG=FG=h,在直角三角形FGE中利用锐角三角函数的定义即可求出h的值,根据三角形的面积公式即可得出结论.
求出△ADE的面积,再判断出△ADE的形状,根据等边三角形的面积求出AE的长,作FG⊥AE于G,由等边三角形及直角三角形的性质判断出△AFG是等腰直角三角形,设AG=FG=h,在直角三角形FGE中利用锐角三角函数的定义即可求出h的值,根据三角形的面积公式即可得出结论.
解:∵AB=2AD,
∴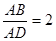
又∵△ABC∽△ADE,△ABC是面积为 ,
,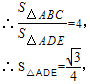
∵△ABC∽△ADE,△ABC是等边三角形,
∴△ADE也是等边三角形,其面积为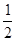 AE•AE•sin60°=
AE•AE•sin60°=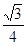 ,即
,即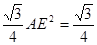 ,解得AE=1,
,解得AE=1,
作FG⊥AE于G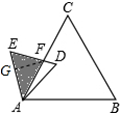
∵∠BAD=45°,∠BAC=∠EAD=60°,
∴∠EAF=45°,
∴△AFG是等腰直角三角形,
设AG=FG=h,在直角三角形FGE中,
∵∠E=60°,EG=1-h,FG=h,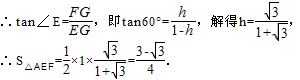
考点:相似三角形的性质,等边三角形的判定,等腰直角三角形的判定
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 ,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q. 的值;
的值; ,AQ=
,AQ= ,求
,求

 (x<0)和
(x<0)和 (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC= ,S△BOC=
,S△BOC= ,则线段AB的长度= .
,则线段AB的长度= .