题目内容
 如图,A是半径为2的⊙O外的一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,则
如图,A是半径为2的⊙O外的一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,则 的长为
的长为
- A.

- B.

- C.π
- D.

A
分析:连接OC、OB,在Rt△OAB中可得出∠A=30°,继而结合题意可判断出△OCB是等边三角形,结合弧长公式即可得出答案.
解答:如图:连接OC、OB,
 在Rt△OAB中,OA=4,OB=2,
在Rt△OAB中,OA=4,OB=2,
故∠OAB=30°,∠AOB=∠3=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴∠4=60°,
 =
= =
= .
.
故选A.
点评:本题考查了弧长的计算及解直角三角形的知识,解答本题的关键是求出△OCB是等边三角形,另外要熟练记忆弧长公式,难度一般.
分析:连接OC、OB,在Rt△OAB中可得出∠A=30°,继而结合题意可判断出△OCB是等边三角形,结合弧长公式即可得出答案.
解答:如图:连接OC、OB,
 在Rt△OAB中,OA=4,OB=2,
在Rt△OAB中,OA=4,OB=2,故∠OAB=30°,∠AOB=∠3=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴∠4=60°,
 =
= =
= .
.故选A.
点评:本题考查了弧长的计算及解直角三角形的知识,解答本题的关键是求出△OCB是等边三角形,另外要熟练记忆弧长公式,难度一般.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
如图,BC是半径为1的⊙O的弦,A为弧BC上一点,M、N分别为BD、AD的中点,则sin∠C的值等于( )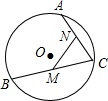

| A、AD | B、BC | C、MN | D、AC |
 如图,
如图, |
| AB |
 |
| BC |
A、s=
| ||||
B、s=
| ||||
C、s=
| ||||
D、s=
|
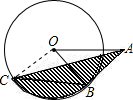 如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连接AC,则图中阴影部分的面积为
如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连接AC,则图中阴影部分的面积为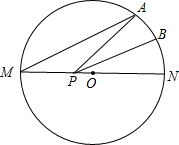 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( ) 如图,P是半径为4的⊙O外一点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.
如图,P是半径为4的⊙O外一点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.