Question

【题目】在中，，现将折叠，使点、两点重合，折痕所在的直线与直线的夹角为，则的大小为__________度.

Answer 1

【答案】或

【解析】

首先根据题意画出图形，如图1，如图1：由翻折的性质可知：EF⊥AB，所以∠A+∠AFE=90°，从而可求得∠A=40°，然后根据等腰三角形的性质和三角形的内角和定理可求得∠B=70°；如图2；由翻折的性质可知：EF⊥AB，∠D+∠DAE=90°，故此∠DAE=40°，然后由等腰三角形的性质和三角形的外角的性质可求得∠B=20°．

如图1：
由翻折的性质可知：EF⊥AB，
∴∠A+∠AFE=90°．
∴∠A=90°-50°=40°，
∵AB=AC，
∴∠B=∠C．
∴∠B=×（180°-∠A）=×(180°40°)=70°；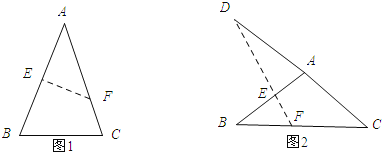

如图2；由翻折的性质可知：EF⊥AB，
∴∠D+∠DAE=90°．
∴∠DAE=90°-50°=40°，
∵AB=AC，
∴∠B=∠C．
∵∠B+∠C=∠DAE，
∴∠B=∠DAE=×40°=20°．

故答案为：或.