题目内容
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且![]() .
.

(1)试判断直线BF与⊙O的位置关系,并说明理由;
(2)若AB=6,BF=8,求![]() .
.
(1)BF为⊙O的切线,理由见解析(2)![]()
解析:(1)证明:连接AE ………………………………………………………1分
∵AB为⊙O的直径,∴∠AEB=90°∴∠BAE+∠ABE=90° …………………2分
∵AB=AC,AE⊥BC ∴AE平分∠BAC ∴![]() ………3分
………3分
∴ ∴AB⊥BF
∴AB⊥BF
∴BF为⊙O的切线 ………………………………………………………5分
(2)过点C作CG⊥BF, 
在Rt△ABF中![]()
∵AC=6 ∴CF=4 ………………7分
∵CG⊥BF,AB⊥BF ∴CG∥AB
∴△GFG∽△AFB ………………8分
∴
∴
∴ ………………………………9分
………………………………9分
在Rt△BCG中![]() ………………………………………………10分
………………………………………………10分
(1)连接AE,利用直径和角的等量代换求得BF为⊙O的切线
(2) 过点C作CG⊥BF,通过△GFG∽△AFB,求得CG、BG的长,从而求得![]()

练习册系列答案
相关题目
 的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.
的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直.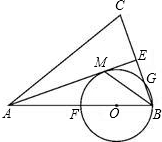 F,FB恰为⊙O的直径.
F,FB恰为⊙O的直径. 7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=
7、如图,在△ABC中,D是BC上的一点,∠C=62°,∠CAD=32°,则∠ADB=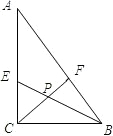 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF平分∠ACB,CF,BE交于点P,AC=4cm,BC=3cm,AB=5cm,则△CPB的面积为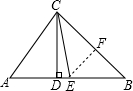 如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为
如图,在△ABC中,CD是高,CE为∠ACB的平分线.若AC=15,BC=20,CD=12,EF∥AC,则∠CEF的大小为