题目内容
已知△ABC为等腰直角三角形,∠C为直角,延长CA至D,以AD为直径作圆,连BD与圆O交于点E,连CE,CE的延长线交圆O于另一点F,那么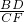 的值等于________.
的值等于________.

分析:连接AE,AF,DF,根据AD为直径,可证A、C、B、E四点共圆,则∠ACF=∠ABD,又∠AFC=∠ADB,可证△AFC∽△ADB,则
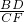 =
= ,而∠FAD=∠FED=∠BEC=∠BAC=45°,根据
,而∠FAD=∠FED=∠BEC=∠BAC=45°,根据 =
=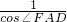 求解.
求解.解答:
 解:如图,连接AE,AF,DF,
解:如图,连接AE,AF,DF,∵AD为直径,
∴∠AED=∠AEB=∠ACB=90°,
∴A、C、B、E四点共圆,
∴∠ACF=∠ABD,
又∵∠AFC=∠ADB,
∴△AFC∽△ADB,
∴
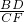 =
= ,
,∵∠FAD=∠FED=∠BEC=∠BAC=45°,
在Rt△ADF中,
 =
=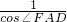 =
=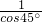 =
= .
.故答案为:
 .
.点评:本题考查了四点共圆的判定与性质,圆周角定理,相似三角形的判定与性质.关键是利用四点共圆,得到圆周角相等,判断相似三角形.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.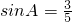 ,其中A为锐角,试求sadA的值;
,其中A为锐角,试求sadA的值;