题目内容
 已知:如图,AD是△ABC的角平分线,且AE=AC,EF∥BC交AC于F.
已知:如图,AD是△ABC的角平分线,且AE=AC,EF∥BC交AC于F.
求证:CE平分∠DEF.
证明:∵AD是△ABC的角平分线,
∴∠EAD=∠CAD,
而AE=AC,AD公共边,
∴△AED≌△ACD,
∴ED=DC,
∴∠CED=∠DCE,
∵EF∥BC,
∴∠FEC=∠ECD,
∴∠CED=∠FEC,
即CE平分∠DEF.
分析:由于AD是△ABC的角平分线,AE=AC,AD公共边,由此可以证明△AED≌△ACD,然后根据全等三角形的性质得到CD=CE,再等腰三角形的性质推出∠CED=∠EDC,又EF∥BC,利用平行线的性质推出∠FEC=∠ECD,等量代换之后即可证明题目结论.
点评:此题主要考查了全等三角形的判定和性质,平行线的性质等知识;有一定的综合性,一般已知角平分线往往是利用角平分线构造全等三角形解决问题.
∴∠EAD=∠CAD,
而AE=AC,AD公共边,
∴△AED≌△ACD,
∴ED=DC,
∴∠CED=∠DCE,
∵EF∥BC,
∴∠FEC=∠ECD,
∴∠CED=∠FEC,
即CE平分∠DEF.
分析:由于AD是△ABC的角平分线,AE=AC,AD公共边,由此可以证明△AED≌△ACD,然后根据全等三角形的性质得到CD=CE,再等腰三角形的性质推出∠CED=∠EDC,又EF∥BC,利用平行线的性质推出∠FEC=∠ECD,等量代换之后即可证明题目结论.
点评:此题主要考查了全等三角形的判定和性质,平行线的性质等知识;有一定的综合性,一般已知角平分线往往是利用角平分线构造全等三角形解决问题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
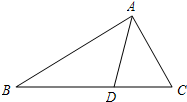 已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )| A、3:2 | B、9:4 | C、2:3 | D、4:9 |
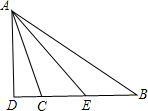 已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
 已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.
已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF. 已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.