题目内容
直线![]() 与坐标轴分别交于
与坐标轴分别交于![]() 两点,动点
两点,动点![]() 同时从
同时从![]() 点出发,同时到达
点出发,同时到达![]() 点,运动停止.点
点,运动停止.点![]() 沿线段
沿线段![]() 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点![]() 沿路线
沿路线![]() →
→![]() →
→![]() 运动.
运动.

(1)直接写出![]() 两点的坐标;
两点的坐标;
(2)设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 时,求出点
时,求出点![]() 的坐标,并直接写出以点
的坐标,并直接写出以点![]() 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点![]() 的坐标.
的坐标.
(1)A(8,0)B(0,6);(2)当0![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
(3)![]() ,M1
,M1![]()
【解析】
试题分析:(1)分别把![]() 、
、![]() 代入
代入![]() 即可求得结果;
即可求得结果;
(2)先根据勾股定理求得AB的长,根据点![]() 由
由![]() 到
到![]() 的时间可求得点
的时间可求得点![]() 的速度,再分当
的速度,再分当![]() 在线段
在线段![]() 上运动(或0
上运动(或0![]() )时,当
)时,当![]() 在线段
在线段![]() 上运动(或
上运动(或![]() )时,两种情况,根据三角形的面积公式求解即可;
)时,两种情况,根据三角形的面积公式求解即可;
(3)把![]() 代入(2)中的函数关系式即可求得点
代入(2)中的函数关系式即可求得点![]() 的坐标,再根据平行四边形的性质求解即可.
的坐标,再根据平行四边形的性质求解即可.
(1)A(8,0)B(0,6);
(2)![]()
![]()
![]() 点
点![]() 由
由![]() 到
到![]() 的时间是
的时间是![]() (秒)
(秒)
![]() 点
点![]() 的速度是
的速度是![]() (单位/秒)
(单位/秒)
当![]() 在线段
在线段![]() 上运动(或0
上运动(或0![]() )时,
)时,![]() ,
,![]()
当![]() 在线段
在线段![]() 上运动(或
上运动(或![]() )时,
)时,![]()
作![]() 于点
于点![]() ,由
,由![]() ,得
,得![]() ,
,
![]() ;
;
(3)![]() ,M1
,M1![]()

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 与坐标轴分别交于
与坐标轴分别交于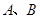 两点,动点
两点,动点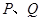 同时从
同时从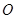 点出发,同时到达
点出发,同时到达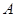 点,运动停止.点
点,运动停止.点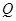 沿线段
沿线段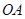 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点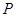 沿路线
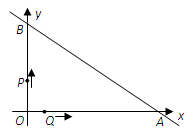
沿路线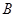 →
→
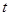 秒,
秒, 的面积为
的面积为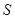 ,求出
,求出 时,求出点
时,求出点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点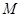 的坐标.
的坐标.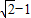 ,直线
,直线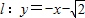 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.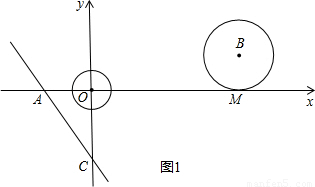
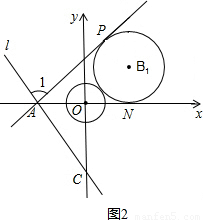
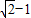 ,直线
,直线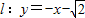 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.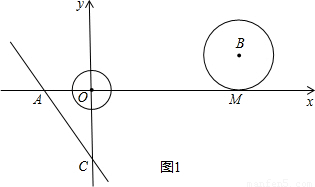

 ,直线
,直线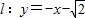 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.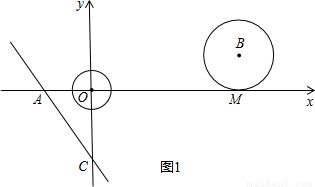

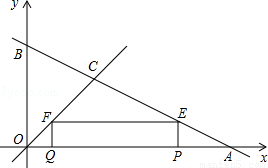
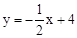 与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).