题目内容
在△ABC的纸片中,∠B=20°,∠C=40°,AC=2,将△ABC沿边BC上的高所在直线折叠后B、C两点之间的距离为________.
2
分析:首先根据题意画出图形,即可得AD⊥BC,点C′是点C沿AD折叠后的对应点,由折叠的性质易得AC′=AC=2,∠AC′D=∠C=40°,继而可得△ABC′是等腰三角形,则可求得将△ABC沿边BC上的高所在直线折叠后B、C两点之间的距离.
解答: 解:如图:AD⊥BC,点C′是点C沿AD折叠后的对应点,
解:如图:AD⊥BC,点C′是点C沿AD折叠后的对应点,
∴AC′=AC=2,∠AC′D=∠C=40°,
∵∠B=20°,
∴∠BAC′=∠AC′D-∠B=40°-20°=20°,
∴∠BAC′=∠B,
∴BC′=AC′=2,
∴将△ABC沿边BC上的高所在直线折叠后B、C两点之间的距离为2.
故答案为:2.
点评:此题考查了折叠的性质以及等腰三角形的判定与性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.
分析:首先根据题意画出图形,即可得AD⊥BC,点C′是点C沿AD折叠后的对应点,由折叠的性质易得AC′=AC=2,∠AC′D=∠C=40°,继而可得△ABC′是等腰三角形,则可求得将△ABC沿边BC上的高所在直线折叠后B、C两点之间的距离.
解答:
 解:如图:AD⊥BC,点C′是点C沿AD折叠后的对应点,
解:如图:AD⊥BC,点C′是点C沿AD折叠后的对应点,∴AC′=AC=2,∠AC′D=∠C=40°,
∵∠B=20°,
∴∠BAC′=∠AC′D-∠B=40°-20°=20°,
∴∠BAC′=∠B,
∴BC′=AC′=2,
∴将△ABC沿边BC上的高所在直线折叠后B、C两点之间的距离为2.
故答案为:2.
点评:此题考查了折叠的性质以及等腰三角形的判定与性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
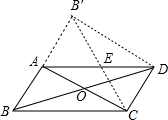 到△AB′C.
到△AB′C.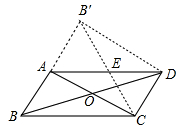
 为顶点的四边形是矩形;
为顶点的四边形是矩形;