Question

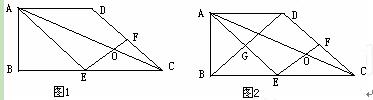
（2011•泰安）已知：在梯形ABCD中，AD∥BC，∠ABC=90°，BC=2AD，E是BC的中点，连接AE、AC．
（1）点F是DC上一点，连接EF，交AC于点O（如图1），求证：△AOE∽△COF；
（2）若点F是DC的中点，连接BD，交AE与点G（如图2），求证：四边形EFDG是菱形．

Answer 1

（1）证明：∵点E是BC的中点，BC=2AD，
∴EC=BE=BC=AD，
又∵AD∥DC，
∴四边形AECD为平行四边形，
∴AE∥DC，
∴∠AEO=∠CFO，∠EAO=∠FCO，
∴△AOE∽△COF；
（2）证明：连接DE，

∵DE平行且等于BE，
∴四边形ABED是平行四边形，
又∠ABE=90°，
∴□ABED是矩形，
∴GE=GA=GB=GD=BD=AE，
∴E、F分别是BC、CD的中点，
∴EF、GE是△CBD的两条中线，
∴EF=BD=GD，GE=CD=DF，
又GE=GD，
∴EF=GD=GE=DF，
∴四边形EFDG是菱形．解析:
略