Question

【题目】定义一种变换：平移抛物线得到抛物线，使经过的顶点．设的对称轴分别交于点，点是点关于直线的对称点．

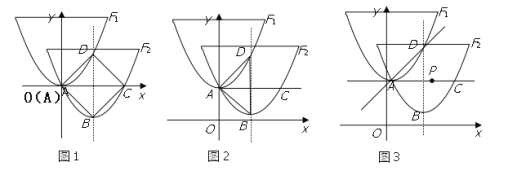
（1）如图1，若：，经过变换后，得到：，点的坐标为，则①的值等于______________；

②四边形为（ ）

A．平行四边形 B．矩形 C．菱形 D．正方形

（2）如图2，若：，经过变换后，点的坐标为，求的面积；

（3）如图3，若，经过变换后，，点是直线上的动点，求点到点的距离和到直线的距离之和的最小值．

Answer 1

【答案】（1）-2；D；（2）2；（3）．

【解析】

试题分析：（1）已知F2的解析式，把已知坐标代入即可得出b的值；

（2）在（1）的基础上求出S△ABD；

（3）要分情况讨论点C在点A的左边还是右边，作PH⊥AD交AD于点H，则PD+PH=PB+PH，是PB+PH值最小可求出h的最小值．

试题解析：（1）-2；D；

（2）∵F2：y=a（x-2）2+c-1，

而A（0，c）在F2上，可得a=．

∴DB=（4a+c）-（c-1）=2，

∴S△ABD=2；

（3）当点C在点A的右侧时（如图1），

设AC与BD交于点N，

抛物线y=x2-x+，配方得y=（x-1）2+2，

其顶点坐标是A（1，2），

∵AC=2，

∴点C的坐标为（1+2，2）．

∵F2过点A，

∴F2解析式为y=（x-1-）2+1，

∴B（1+，1），

∴D（1+，3）

∴NB=ND=1，

∵点A与点C关于直线BD对称，

∴AC⊥DB，且AN=NC

∴四边形ABCD是菱形．

∴PD=PB．

作PH⊥AD交AD于点H，则PD+PH=PB+PH．

要使PD+PH最小，即要使PB+PH最小，

此最小值是点B到AD的距离，即△ABD边AD上的高h．

∵DN=1，AN=，DB⊥AC，

∴∠DAN=30°，

故△ABD是等边三角形．

∴h=AD=∴最小值为．

当点C在点A的左侧时（如图2），同理，最小值为．

综上，点P到点D的距离和到直线AD的距离之和的最小值为．