题目内容
 如图所示,在直线上一点O引一条射线OC,其中OB平分∠AOC,OD平分∠COE,说明BO与DO的关系?
如图所示,在直线上一点O引一条射线OC,其中OB平分∠AOC,OD平分∠COE,说明BO与DO的关系?
分析:结合图形,根据垂直的定义,只要证明∠BOD=90°,即可得BO⊥DO.
解答:解:BO⊥DO.
理由:∵OB平分∠AOC,OD平分∠COE,
∴∠BOC+∠COD=
∠AOC+
∠COE=
(∠AOC+∠COE)=
×180°=90°,
∴OD⊥OE.
理由:∵OB平分∠AOC,OD平分∠COE,
∴∠BOC+∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OD⊥OE.
点评:本题主要考查垂直的定义和角平分线的定义,属于基础题型.利用角平分线的性质证明∠BOD=90°是解答本题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 ,顶点A所经过的路线长等于________.
,顶点A所经过的路线长等于________.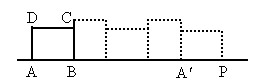
 ,顶点A所经过的路线长等于________.
,顶点A所经过的路线长等于________.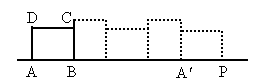
 如图所示,在直线上一点O引一条射线OC,其中OB平分∠AOC,OD平分∠COE,说明BO与DO的关系?
如图所示,在直线上一点O引一条射线OC,其中OB平分∠AOC,OD平分∠COE,说明BO与DO的关系?