题目内容
以长为2cm的定线段AB为边，作正方形ABCD，取AB的中点P．在BA的延长线上取点F，使PF=PD，以AF为边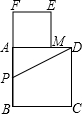
作正方形AMEF，点M落在AD上，如图所示．（1）试求AM、DM的长；
（2）点M是线段AD的黄金分割点吗？请说明理由．
分析：（1）要求AM的长，即是求AF的长，只需求得PF的长，根据勾股定理进行计算PD的长就可；要求DM的长，只需AD-AM就可；
（2）根据黄金分割点的定义，只需证明AM2=AD•DM．
（2）根据黄金分割点的定义，只需证明AM2=AD•DM．
解答：解：（1）在Rt△APD中，AP=1cm，AD=2cm，
由勾股定理知PD=
=
=
cm，
∴AM=AF=PF-AP=PD-AP=
-1（cm）
DM=AD-AM=3-
（cm）；
（2）∵AM2=（
-1）2=6-2
，
AD•DM=2×（3-
）=6-2
，
∴AM2=AD•DM，
所以点M是线段AD的黄金分割点．
由勾股定理知PD=
| AD2+AP2 |
| 4+1 |
| 5 |
∴AM=AF=PF-AP=PD-AP=
| 5 |
DM=AD-AM=3-
| 5 |
（2）∵AM2=（
| 5 |
| 5 |
AD•DM=2×（3-
| 5 |
| 5 |
∴AM2=AD•DM，
所以点M是线段AD的黄金分割点．
点评：能够根据已知条件结合勾股定理求得线段的长，能够用黄金分割点的定义进行证明．
练习册系列答案
相关题目
作正方形AMEF，点M落在AD上，如图所示．
