题目内容
9.一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
分析 (1)根据列表,可得答案;
(2)游戏是否公平,求出游戏双方获胜的概率,比较是否相等.
解答 解:列举所有可能:
| 甲 | 0 | 1 | 2 |
| 乙 | 1 | 0 | 0 |
| 2 | 2 | 1 |
由表可知甲获胜的概率=$\frac{1}{3}$,乙获胜的概率=$\frac{2}{3}$,
乙获胜的可能性大,
所以游戏是不公平的.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
20.中共中央、国务院近日印发的《国家创新驱动发展战略纲要》强调,要增强企业创新能力,发展壮大创新型企业家群体,推动创新创业,激发全社会创造活力.据悉,2015年全社会研发资金达14 000多亿元.将14 000用科学记数法表示应为( )
| A. | 0.14×105 | B. | 1.4×104 | C. | 1.4×105 | D. | 0.14×106 |

 如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=70°.
如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3=70°. 如图,矩形ABCD的面积是15,边AB的长比AD的长大2,则AD的长是3.
如图,矩形ABCD的面积是15,边AB的长比AD的长大2,则AD的长是3. 如图是由六个相同的小正方体搭成的几何体,这个几何体的主视图是( )
如图是由六个相同的小正方体搭成的几何体,这个几何体的主视图是( )



 如图,AC是?ABCD的对角线,∠BAC=∠DAC.
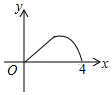
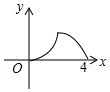
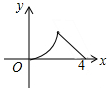
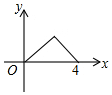
如图,AC是?ABCD的对角线,∠BAC=∠DAC.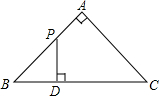 如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )