题目内容
如图所示,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G。
(1)求证:△BDG∽△DEG;
(2)若EG·BG=4,求BE的长。

(1) 3分

证明:∵∠BEC=∠DEG,∠CBE=∠GDE ∴△BDG∽△DEG;
(2) 5分
∵△BCE≌△DCF ∴B、C、F三点共线
又∠DBC=∠BDC=450 ∴∠DBE=∠EBC=∠CDF=22.50 ∴∠BDF=67.50 ∠F=67.50
∴∠BDF=∠F BE平分∠DBC ∴G为DF的中点 ∴DF=2DC=BE
又 ∵△BDG∽△DEG ∴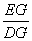 =
=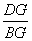 ∴DG2= EG·BG=4
∴DG2= EG·BG=4
∴DG=2 ∴BE=2DG=4

练习册系列答案
相关题目
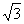




 烟花侧面包装纸的面积至少需要(解缝面积不计)( )
烟花侧面包装纸的面积至少需要(解缝面积不计)( )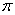 rh B. 24rh+
rh B. 24rh+
 ,
, 的中点.
的中点.
