题目内容
若干个正方形和等腰直角三角形拼接成如图所示的图形，若最大的正方形的边长是7cm，则正方形A、B、C、D的面积和是
- A.14cm2
- B.42cm2
- C.49cm2
- D.64cm2
C
分析：正方形A与正方形B的面积和，由勾股定理可得为正方形M的面积，同理可得正方形C与正方形D的面积和为正方形N的面积，正方形M与正方形N的面积和为正方形H的面积，已知正方形H的边长，从而不难求解．
解答：
解：∵正方形A，B的边长分别是直角三角形E两直角边，
∴SA+SB=SM，
同理：SC+SD=SN，SM+SN=SH，
∵正方形H的边长为7cm，
∴正方形H的面积=49cm2，
即正方形A、B、C、D的面积和为：49cm2，
故选C．
点评：此题主要考查勾股定理，正方形的性质及等腰直角三角形的性质的综合运用．
分析：正方形A与正方形B的面积和，由勾股定理可得为正方形M的面积，同理可得正方形C与正方形D的面积和为正方形N的面积，正方形M与正方形N的面积和为正方形H的面积，已知正方形H的边长，从而不难求解．
解答：
解：∵正方形A，B的边长分别是直角三角形E两直角边，∴SA+SB=SM，
同理：SC+SD=SN，SM+SN=SH，
∵正方形H的边长为7cm，
∴正方形H的面积=49cm2，
即正方形A、B、C、D的面积和为：49cm2，
故选C．
点评：此题主要考查勾股定理，正方形的性质及等腰直角三角形的性质的综合运用．
练习册系列答案
全优点练单元计划系列答案
相关题目
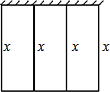周长为48m的篱笆，一面利用旧墙围成如图所示的矩形花圃：①写出花圃面积y与x的函数关系式；②给出x的取值范围；③求宽x为何值时，花圃的面积最大？
=2，a=|-3|，那么b-a的值是
，3.14，
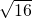，-π，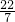
，5.121121121…中无理数有
图中的几何体是由7个大小相同的小正方体组成的，该几何体的俯视图为
