题目内容
 已知:如图,等腰梯形ABCD,AD=1,AD∥BC,沿对角线AC翻折梯形ABCD,若点D恰好落在下底BC的上点E处.
已知:如图,等腰梯形ABCD,AD=1,AD∥BC,沿对角线AC翻折梯形ABCD,若点D恰好落在下底BC的上点E处.
(1)求证:四边形AECD是菱形;
(2)当∠B=60°时,求梯形ABCD的面积.
(1)证明:∵△ADC沿AC翻折得△AEC,
∴△ADC≌△AEC,
∴AE=AD,EC=DC,∠EAC=∠DAC,
∵AD∥BC,
∴∠DAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=EC=AD=CD,
∴四边形AECD是菱形;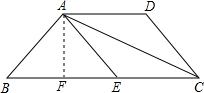
(2)解:∵梯形ABCD是等腰梯形,
∴AB=CD,
∵AE=EC=AD=CD,AD=1,
∴AB=AE,
∵∠B=60°,
∴△ABE是等边三角形,
∴AD=BE=EC=1,
∴BC=2,
作AF⊥BE,
∴AF= ,
,
∴S梯形ABCD=(AD+BC)×AF÷2
=(1+2)× ÷2
÷2
=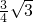 .
.
分析:(1)根据翻折的性质和等腰梯形的性质,只要证得AD=CD=EC=AE,即可证明;
(2)易证△ABE是等边三角形,可得AD=AB=BE=1,作出高并求得AF= ,然后根据梯形面积的求法,解答出即可.
,然后根据梯形面积的求法,解答出即可.
点评:本题主要考查了等腰梯形的性质、菱形的判定和翻折变换,对于菱形的证明,注意选择合适的条件.
∴△ADC≌△AEC,
∴AE=AD,EC=DC,∠EAC=∠DAC,
∵AD∥BC,
∴∠DAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=EC=AD=CD,
∴四边形AECD是菱形;

(2)解:∵梯形ABCD是等腰梯形,
∴AB=CD,
∵AE=EC=AD=CD,AD=1,
∴AB=AE,
∵∠B=60°,
∴△ABE是等边三角形,
∴AD=BE=EC=1,
∴BC=2,
作AF⊥BE,
∴AF=
 ,
,∴S梯形ABCD=(AD+BC)×AF÷2
=(1+2)×
 ÷2
÷2=
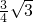 .
.分析:(1)根据翻折的性质和等腰梯形的性质,只要证得AD=CD=EC=AE,即可证明;
(2)易证△ABE是等边三角形,可得AD=AB=BE=1,作出高并求得AF=
 ,然后根据梯形面积的求法,解答出即可.
,然后根据梯形面积的求法,解答出即可.点评:本题主要考查了等腰梯形的性质、菱形的判定和翻折变换,对于菱形的证明,注意选择合适的条件.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
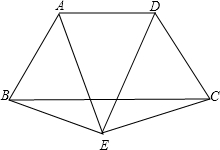 已知:如图,等腰梯形ABCD中,AB=CD,AD∥BC,E是梯形外一点,且EA=ED,求证:EB=EC.
已知:如图,等腰梯形ABCD中,AB=CD,AD∥BC,E是梯形外一点,且EA=ED,求证:EB=EC. 20、已知:如图,等腰梯形ABCD中,AB∥DC,E为DC的中点,求证:∠EAB=∠EBA.
20、已知:如图,等腰梯形ABCD中,AB∥DC,E为DC的中点,求证:∠EAB=∠EBA. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 已知,如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13
已知,如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13