Question

【题目】在平面直角坐标系中，点的坐标为.

（1）如图1，若点的坐标为，是等腰直角三角形，，，求点坐标；

（2）如图2，若点是的中点，求证：；

（3）如图3，是等腰直角三角形，，，是等边三角形，连接，若，求点坐标.

Answer 1

【答案】（1）（7，3）；（2）见详解；（3）（2，0）.

【解析】

（1）过点C作CM⊥x轴于点M，由△ABC是等腰直角三角形，则AB=BC，然后证明△AOB≌△BMC，得到AO=BM，OB=CM，即可求出点C的坐标；

（2）根据题意，△ABO是直角三角形，点E是AB中点，即可得到；

（3）根据题意，把△DAO绕着点D旋转60°得到△DCG，作CM⊥BG与M，则△DAO≌△DCG，得到∠AOD=∠CGD=30°，CG=OA=4，然后得到△ODG是等边三角形，求出∠CGM=30°，得到，再由△AOB≌△BMC，得到OB=CM=2，即可得到点B的坐标.

解：（1）如图，过点C作CM⊥x轴于点M，则∠BMC=90°=∠AOB，

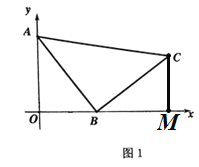
∵点A为（0，4），点B为（3，0），

∴OA=4，OB=3，

∵AB=BC，∠ABC=90°，

∴∠ABO+∠CBM=90°，∠BCM+∠CBM=90°，

∴∠ABO=∠BCM，

∴△AOB≌△BMC，

∴OA=BM，OB=CM=3，

∴OM=OB+BM=3+4=7，

∴点C的坐标为：（7，3）；

（2）如图，

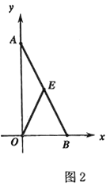
∵△AOB是直角三角形，点E是AB的中点，

∴OE=OA=OB=，

∴；

（3）根据题意，如图，把△DAO绕着点D旋转60°，得到△DCG，作CM⊥BG与M，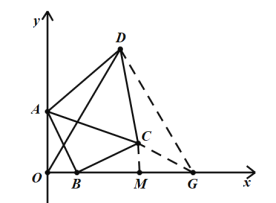

则△DAO≌△DCG，

∴∠AOD=∠CGD=30°，CG=OA=4，

∵OD=DG，∠ODG=60°，

∴△ODG是等边三角形，

∴∠OGD=60°，

∴∠CGM=60°-30°=30°，

在Rt△CGM中，CM=，

由（1）知，△AOB≌△BMC，

∴OB=CM，

∴OB=2，

∴点B的坐标为：（2，0）.