题目内容
抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,与y轴交于C点,且线段AB的长为1,△ABC的面积为1,则b的值为________.
-3
分析:设A,B,C三点的坐标分别为(x1,0)、(x2,0)、(0,c),再由线段AB的长为1,△ABC的面积为1可求出c的值,再由根与系数的关系及线段AB的长度列出方程组即可求出b的值.
解答:设A,B,C三点的坐标分别为(x1,0)、(x2,0)、(0,c),且x1<x2,
∵抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,线段AB的长为1,
∴x2-x1=1,
∵△ABC的面积为1,即 (x2-x1)•|c|=1,
(x2-x1)•|c|=1,
∴c=±2,
∵x1>0、x2>0,
∴x1•x2,>0,
∵x1•x2=c,
∴c=2,
∴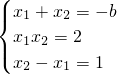 ,
,
解得b=±3,
∵x1>0、x2>0,
∴x1+x2>0,
∵x1+x2=-b,
∴b<0,
∴b=-3.
故答案为:-3.
点评:本题考查的是抛物线与x轴的交点及根与系数的关系、三角形的面积公式,在解答此类题目时要注意判断未知数的正负,这是此类题目的易错点.
分析:设A,B,C三点的坐标分别为(x1,0)、(x2,0)、(0,c),再由线段AB的长为1,△ABC的面积为1可求出c的值,再由根与系数的关系及线段AB的长度列出方程组即可求出b的值.
解答:设A,B,C三点的坐标分别为(x1,0)、(x2,0)、(0,c),且x1<x2,
∵抛物线y=x2+bx+c与x轴的正半轴交于A,B两点,线段AB的长为1,
∴x2-x1=1,
∵△ABC的面积为1,即
 (x2-x1)•|c|=1,
(x2-x1)•|c|=1,∴c=±2,
∵x1>0、x2>0,
∴x1•x2,>0,
∵x1•x2=c,
∴c=2,
∴
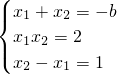 ,
,解得b=±3,
∵x1>0、x2>0,
∴x1+x2>0,
∵x1+x2=-b,
∴b<0,
∴b=-3.
故答案为:-3.
点评:本题考查的是抛物线与x轴的交点及根与系数的关系、三角形的面积公式,在解答此类题目时要注意判断未知数的正负,这是此类题目的易错点.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
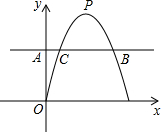 且与直线AB交于另一点C(在B的左边),抛物线的顶点为P.
且与直线AB交于另一点C(在B的左边),抛物线的顶点为P.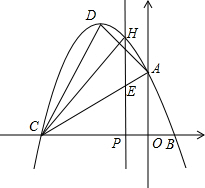 已知:m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点B(m,0),A(0,n)
已知:m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图象经过点B(m,0),A(0,n)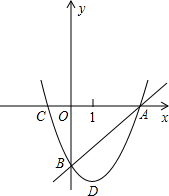 (2013•普陀区二模)如图,抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(2013•普陀区二模)如图,抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A、B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.