题目内容
5.因连续大雨,某段公路遭山体滑坡,早上八点半,有关部门立即组织人员进行清理.若人工清理,4小时后,再换大型机械清理,则大型机械用3.6小时可以清理完毕,已知大型机械清理的效率是人工的10倍.(1)若单独由人工清理需要几小时;
(2)若人工清理每小时费用200元,机械清理每小时2400元,为确保在下午五点前(含五点)清理完毕,怎样安排人工和机械可使总费用最低(人工清理和机械清理不能同时进行)
分析 (1)根据题意设单独由人工清理需要x小时,则单独由大型机械清理需要$\frac{x}{10}$小时,利用工作时间以及工作效率得出等式求出即可;
(2)利用人工与机械每小时所需费用得出人工清理安排时间越长,总费用越低,进而利用总时间8.5小时,再利用总工作量为1得出等式求出即可.
解答 解:(1)设单独由人工清理需要x小时,则单独由大型机械清理需要$\frac{x}{10}$小时,根据题意可得:
$\frac{4}{x}$+$\frac{3.6}{\frac{x}{10}}$=1,
解得:x=40,
经检验得:x=40是原方程的根,
答:单独由人工清理需要40小时;
(2)由题意可得:早上八点半到下午五点是8.5小时,
∵人工清理每小时费用200元,机械清理每小时2400元,
∴人工清理安排时间越长,总费用越低,
设安排人工y小时,则机械清理(8.5-y)小时,
故$\frac{y}{40}$+$\frac{8.5-y}{4}$=1,
解得:y=5.
即安排人工清理5小时,机械清理3.5小时,此时总费用最低.
点评 此题主要考查了分式方程的应用以及一元一次方程的应用,根据题意结合总工作量为1得出等式是解题关键.

练习册系列答案
相关题目
13.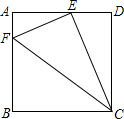 如图,在正方形ABCD中,E是AD的中点,F是AB边上一点,BF=3AF,则下列四个结论:
如图,在正方形ABCD中,E是AD的中点,F是AB边上一点,BF=3AF,则下列四个结论:
①△AEF∽△DCE;
②CE平分∠DCF;
③点B、C、E、F四个点在同一个圆上;
④直线EF是△DCE的外接圆的切线;
其中,正确的个数是( )
 如图,在正方形ABCD中,E是AD的中点,F是AB边上一点,BF=3AF,则下列四个结论:
如图,在正方形ABCD中,E是AD的中点,F是AB边上一点,BF=3AF,则下列四个结论:①△AEF∽△DCE;
②CE平分∠DCF;
③点B、C、E、F四个点在同一个圆上;
④直线EF是△DCE的外接圆的切线;
其中,正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.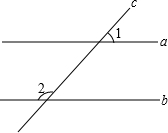 如图,已知,直线a∥b,∠1=36°,则∠2等于( )
如图,已知,直线a∥b,∠1=36°,则∠2等于( )
 如图,已知,直线a∥b,∠1=36°,则∠2等于( )
如图,已知,直线a∥b,∠1=36°,则∠2等于( )| A. | 36° | B. | 54° | C. | 126° | D. | 144° |
10.下列方程的解是x=1的是( )
| A. | $\frac{x-1}{2}$=10 | B. | 2-x=2x-1 | C. | $\frac{2}{x}$+1=0 | D. | x2=2 |