题目内容
 已知:如图,在△ABC中,AD是BC边上的中线,∠B=30°,∠C=45°,AC=4.求BC的长和tan∠ADC的值.
已知:如图,在△ABC中,AD是BC边上的中线,∠B=30°,∠C=45°,AC=4.求BC的长和tan∠ADC的值.
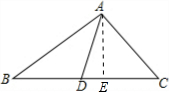 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,∴∠AEC=∠AEB=90°,
在Rt△AEC中,
∵AC=4,
∴cos∠C=
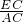 ,即cos45°=
,即cos45°=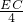 ,
,∴EC=4×cos45°=2
 ,
,又∵∠C=45°,
∴AE=EC=2
 ,
,在Rt△AEB中,
tan∠B=
 ,即tan30°=
,即tan30°=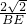 ,
,∴BE=
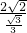 =2
=2 ,
,∴BC=BE+EC=2
 +2
+2 ,
,∴DE=DC-EC=
 BC-EC=
BC-EC= (2
(2 +2
+2 )-2
)-2 =
= -
- ,
,∴tan∠ADC=
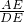 =
=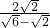 =
= +1.
+1.分析:首先作AE⊥BC,构建直角三角形,然后根据直角三角形特殊角的三角函数,即可推出EC和AE的长度,再根据∠B的正切值推出BE的长度,既而推出BC和C、BD的长度,便知DE=DC-EC=
 BC-EC=
BC-EC=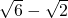 ,根据正切的定义,即可推出tan∠ADC的值.
,根据正切的定义,即可推出tan∠ADC的值.点评:本题主要考查解直角三角形、特殊角的三角函数值,关键在于根据题意作出辅助线构建直角三角形,推出AE,DE的长度.

练习册系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,