题目内容
解方程: .
.
解:设y=x2-2x,则原方程化为y2-y-6=0.
即(y-3)(y+2)=0,
解得y1=-2,y2=3.
当y1=-2时,x2-2x=-2,无解,
当y2=3时,x2-2x=3.
解得x1=3,x2=-1,
检验:当x1=3时,9-6- =3-2=1,
=3-2=1,
当x2=-1时,1+2-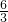 =3-2=1,
=3-2=1,
x1=3,x2=-1都是原方程的根,
∴原方程的根是x1=3,x2=-1.
分析:可根据方程特点设y=x2-2x,则原方程可化为y2-y-6=0.解一元二次方程求y,再求x.
点评:本题考查用换元法解分式方程的能力,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.
即(y-3)(y+2)=0,
解得y1=-2,y2=3.
当y1=-2时,x2-2x=-2,无解,
当y2=3时,x2-2x=3.
解得x1=3,x2=-1,
检验:当x1=3时,9-6-
 =3-2=1,
=3-2=1,当x2=-1时,1+2-
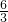 =3-2=1,
=3-2=1,x1=3,x2=-1都是原方程的根,
∴原方程的根是x1=3,x2=-1.
分析:可根据方程特点设y=x2-2x,则原方程可化为y2-y-6=0.解一元二次方程求y,再求x.
点评:本题考查用换元法解分式方程的能力,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.

练习册系列答案
相关题目