题目内容
如图，已知点A（2，4），B（4，m）是反比例函数y=| k | x |
分析：首先根据A点坐标求得反比例函数的解析式，进而可确定点B的坐标；取B点关于x轴的对称点B′，易得B′的坐标，进而可求得直线AB′的解析式，若PA+PB最小，即PA+PB′最小，根据两点间线段最短可知：点P为直线AB′与x轴的交点，由此得解．
解答：解：将A（2，4）代入反比例函数解析式中，得：k=xy=8，即y=
；
∴B（4，2）；
取B点关于x轴的对称点B′（4，-2）；
易求得直线AB′：y=-3x+10；
若PA+PB最小，那么P点即为直线AB′与x轴的交点，
∴P（
，0）．
故答案为：（
，0）．
| 8 |
| x |
∴B（4，2）；
取B点关于x轴的对称点B′（4，-2）；
易求得直线AB′：y=-3x+10；
若PA+PB最小，那么P点即为直线AB′与x轴的交点，
∴P（
| 10 |
| 3 |
故答案为：（
| 10 |
| 3 |
点评：此题考查了反比例函数、一次函数解析式的确定，以及平面展开-最短路径问题，找出点P的位置是解决此题的关键．
练习册系列答案
相关题目
16、如图，已知点D是∠ABC的平分线上一点，点P在BD上，PA⊥AB，PC⊥BC，垂足分别为A，C、下列结论错误的是（ ）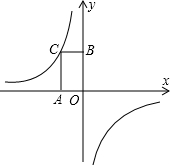
如图，已知点C为反比例函数y=-
如图，已知点A、B、C、D均在已知圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10cm．图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
如图，已知点D为△ABC中AC边上一点，且AD：DC=3；4，设
如图，已知点C为AB上一点，AC=12cm，CB=